数列{an}的前n项和为Sn(n∈N+),点(an,Sn)在直线y=2x-3n.
(1)求数列{an}的通项公式;
(2)数列{an}中是否存在三项,它们可以构成等差数列?若存在,请求出一组适合条件的项;若不存在,请说明理由.
解:(1)由题意,∵数列{a
n}的前n项和为S
n(n∈N
+),点(a
n,S
n)在直线y=2x-3n.
∴S
n=2a
n-3n①,S
n+1=2a
n+1-3(n+1)②
②-①化简可得a
n+1=2a
n+3,…(3分)
∴a
n+1+3=2(a
n+3)
∴数列{a
n+3}是公比为2的等比数列
∵a
1=S
1=2a
1-3,∴a
1=3
∴a
1+3=3+3=6
∴

∴
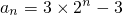
…(6分)
(2)设存在s,p,r∈N
+且s<p<r,使a
s,a
p,a
r成等差数列,…(7分)
∴2a
p=a
s+a
r,即 2(3×2
p-3)=(3×2
s-3)+(3×2
r-3)
∴2
p+1=2
s+2
r∴2
p-s+1=2
r-s+1 (*) …(10分)
∵s、p、r∈N
+且s<p<r
∴2
p-s+1、2
r-s为偶数
∵1+2
r-s为奇数,(*)式产生矛盾.所以这样的三项不存在.…(13分)
分析:(1)根据数列{a
n}的前n项和为S
n(n∈N
+),点(a
n,S
n)在直线y=2x-3n,可得S
n=2a
n-3n,再写一式,两式相减,整理可得数列{a
n+3}是公比为2的等比数列,从而可求数列{a
n}的通项公式;
(2)设存在s,p,r∈N
+且s<p<r,使a
s,a
p,a
r成等差数列,可得出2
p-s+1=2
r-s+1,利用2
p-s+1、2
r-s为偶数,而1+2
r-s为奇数,即可得出结论.
点评:本题考查数列的通项,考查数列与汗水的关系,考查构造法求等比数列,考查存在性问题的探究,有综合性.


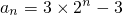 …(6分)
…(6分)

 阅读快车系列答案
阅读快车系列答案