
| 1 |
| 2 |
| 1 |
| 2 |
| ρ2 |
| 2 |
| ρ2 |
| 2 |
| ρ2 |
| 4 |
| ρ2 |
| 2 |
| 2c2 |
| sin2α |
| 2c2 |
| sin2α |
| 2c2 |
| sin2α |


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:
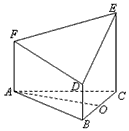
 如图所示的几何体是由以等边三角形ABC为底面的棱柱被平面DEF所截而得,已知FA⊥
如图所示的几何体是由以等边三角形ABC为底面的棱柱被平面DEF所截而得,已知FA⊥查看答案和解析>>
科目:高中数学 来源: 题型:044
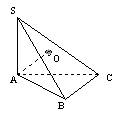
如图,已知△ABC是锐角三角形,SA⊥平面ABC,连结SB和SC,得到△SBC,过A作AO⊥平面SBC,O是垂足,求证:O不是△SBC的垂心.
查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:044
查看答案和解析>>
科目:高中数学 来源:成功之路·突破重点线·数学(学生用书) 题型:047
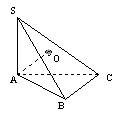
如图,已知△ABC是锐角三角形,SA⊥平面ABC,连结SB和SC,得△SBC,过作A作AO⊥平面SBC,O是垂足.求证:O不是△SBC的垂心.

查看答案和解析>>
科目:高中数学 来源:山东省模拟题 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com