练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    对平面内两定点A、B及动点P,有以下两个命题:p:|PA|+|PB|是定值;q:点P的轨迹是以A、B为焦点的椭圆.则p是q的(    )

    A.充分不必要条件                        B.必要不充分条件

    C.充要条件                                 D.既不充分又不必要条件

    B

    解析：pq,pq.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    设平面内两向量
    a
    ，
    b
    满足：
    a
    ⊥
    b
    ，|
    a
    |=2，|
    b
    |=1    ，点M（x，y）的坐标满足：x
    a
    +(y2-4)
    b
    与-x
    a
    +
    b
    互相垂直．求证：平面内存在两个定点A、B，使对满足条件的任意一点M均有|||
    MA
    |-|
    MB
    ||    等于定值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    平面内与两定点A1（-2，0），A2（2，0）连线的斜率之积等于非零常数m的点的轨迹，加上A1，A2两点，所成的曲线C可以是圆，椭圆或双曲线．
    （I）求曲线C的方程，并讨论C的形状与m值的关系．
    （Ⅱ）当m=-1时，对应的曲线为C1；对给定的m∈（-∞，-1），对应的曲线为C2，若曲线C1的斜率为1的切线与曲线C2相交于A，B两点，且
    OA
    •
    OB
    =2    （O为坐标原点），求曲线C2的方程．

    查看答案和解析>>

    科目：高中数学 来源：高考零距离　二轮冲刺优化讲练　数学 题型：047

    设平面内两向量a、b满足：a⊥b，｜a｜＝2，｜b｜＝1，点M(x，y)的坐标满足：xa＋(y2－4)b与－xa＋b互相垂直．

    求证：平面内存在两个定点A、B，使对满足条件的任意一点M均有｜｜｜－｜｜｜等于定值．

    查看答案和解析>>

    科目：高中数学 来源：2011年高三数学复习（第8章 圆锥曲线）：8.10 向量在解析几何中的应用（解析版） 题型：解答题

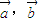    设平面内两向量满足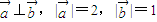：，点M（x，y）的坐标满足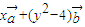：与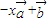互相垂直．求证：平面内存在两个定点A、B，使对满足条件的任意一点M均有|等于定值．

    查看答案和解析>>

    同步练习册答案