
已知函数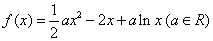
(Ⅰ)若函数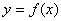 存在极大值和极小值,求
存在极大值和极小值,求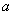 的取值范围;
的取值范围;
(Ⅱ)设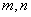 分别为
分别为 的极大值和极小值,其中
的极大值和极小值,其中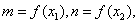 且
且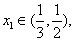 求
求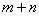 的取值范围.
的取值范围.
解:(Ⅰ) 其中
其中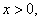
由题设知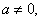 且关于
且关于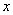 的方程
的方程 有两个不相等的正数根,…… 1分
有两个不相等的正数根,…… 1分
记为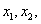 满足
满足 化简得
化简得
经检验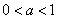 满足题设,故为所求;…… 4分
满足题设,故为所求;…… 4分
(Ⅱ)方法一:由题设结合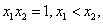 知
知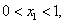
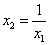 , ……………5分
, ……………5分
且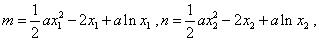
所以
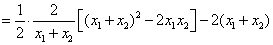
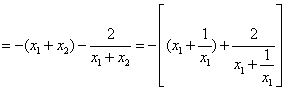 , ……………7分
, ……………7分
因为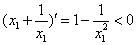 ,所以
,所以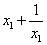 在区间
在区间 是减函数,
是减函数,
所以 ……………8分
……………8分
设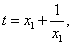 且
且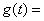
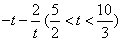 ,
,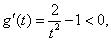
所以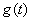 在区间
在区间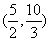 上是减函数, ……………9分
上是减函数, ……………9分
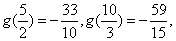 所以
所以
因此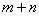
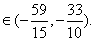 ……………11分
……………11分
方法二:由题设结合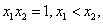 知
知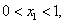
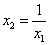 , ……………5分
, ……………5分
且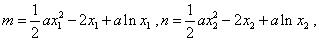
所以
 , ……………7分
, ……………7分
设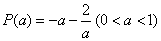 ,
,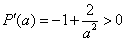 ,
,
所以 在区间
在区间 上是增函数, ……………8分
上是增函数, ……………8分
而 ,设
,设 ,则
,则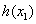 在
在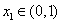 时是增函数,
时是增函数,
所以当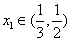 时,
时,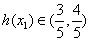 ,即
,即 , ……………9分
, ……………9分
所以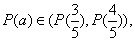 且
且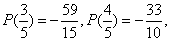
因此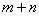
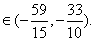 ……………11分
……………11分
方法三:由方法一知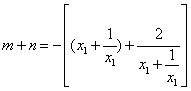
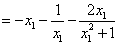 …………7分
…………7分
设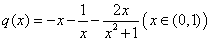 ,则
,则


所以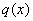 在区间
在区间 上是增函数, ……………9分
上是增函数, ……………9分
而
所以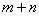
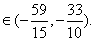 ……………11分
……………11分
方法四:前同方法二知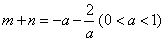 , ……………7分
, ……………7分
当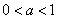 时,关于
时,关于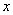 的方程
的方程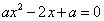 有两个不相等的正数根
有两个不相等的正数根
那么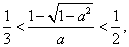 即
即 解得
解得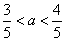 , ……………9分
, ……………9分
下同方法二.


科目:高中数学 来源: 题型:
如图,先将边长为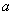 的正方形铁皮的四个角各截去一个边长为
的正方形铁皮的四个角各截去一个边长为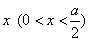 的小正方形,然后沿虚线折成一个无盖的长方体盒子.设长方体盒子的体积是
的小正方形,然后沿虚线折成一个无盖的长方体盒子.设长方体盒子的体积是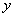 ,则
,则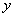 关于
关于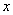 的函数关系式为
的函数关系式为
A. B.
B.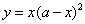
C.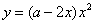 D.
D.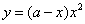

查看答案和解析>>
科目:高中数学 来源: 题型:
.小强和小华两位同学约定下午在武荣公园篮球场见面,约定谁先到后必须等10分钟,这时若
另一人还没有来就可以离开.如果小强是1:40分到达的,假设小华在1点到3点内到达,且
小华在 1点到3点之间何时到达是等可能的,则他们会面的概率是
A.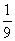 B.
B.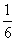 C.
C. 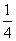 D.
D.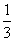
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com