
如图,已知在四棱锥P﹣ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E,F,G分别是PD,PC,BC的中点.
(1)求证:平面EFG⊥平面PAD;
(2)若M是线段CD上一点,求三棱锥M﹣EFG的体积.
(1)详见解析;(2)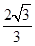 .
.
解析试题分析:(1)要证明面面垂直,只需在一个平面内找到另一平面的一条垂线.由已知平面 平面
平面 ,且
,且 ,可证
,可证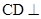 平面
平面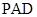 ,再根据
,再根据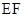 是中位线,可证
是中位线,可证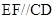 ,从而
,从而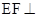 平面
平面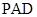 ,进而再证平面
,进而再证平面 平面
平面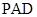 ,该题实质是先找到面
,该题实质是先找到面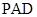 的一条垂线
的一条垂线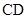 ,再将
,再将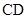 平移到面
平移到面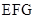 内;
内;
(2)点 是线段
是线段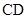 的动点,考虑到
的动点,考虑到 和
和 到面
到面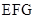 的距离相等,故
的距离相等,故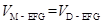 ,再结合第(1)问结果,取
,再结合第(1)问结果,取 的中点
的中点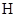 连接
连接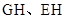 ,据面面垂直的性质,点
,据面面垂直的性质,点 到
到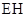 的距离就是三棱锥
的距离就是三棱锥 的高,再求
的高,再求 ,进而求体积.
,进而求体积.
试题解析:(1)∵平面 平面
平面 ,平面
,平面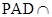 平面
平面 ,
,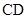
 平面
平面 ,
, ,
, 平面
平面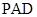 ,又
,又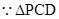 中,
中, 分别是
分别是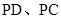 的中点,
的中点,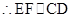 ,可得
,可得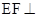 平面
平面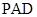 ,
,
 平面
平面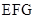 ,∴平面
,∴平面 平面
平面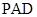 ;
;
(2)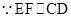 ,
,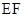
 平面
平面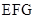 ,
,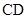
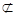 平面
平面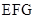 ,
,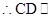 平面
平面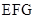 ,因此
,因此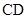 上的点
上的点 到平面
到平面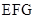 的距离等于点
的距离等于点 到平面
到平面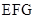 的距离,∴
的距离,∴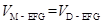 ,取
,取 的中点
的中点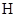 连接
连接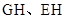 ,则
,则 ,
,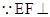 平面
平面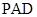 ,
,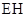
 平面
平面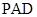 ,∴
,∴ ,于是
,于是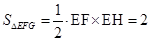 ,
,
∵平面 平面
平面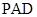


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案科目:高中数学 来源: 题型:解答题
如图,在长方体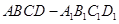 中,
中,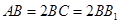 , 沿平面
, 沿平面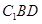 把这个长方体截成两个几何体: 几何体(1);几何体(2)
把这个长方体截成两个几何体: 几何体(1);几何体(2)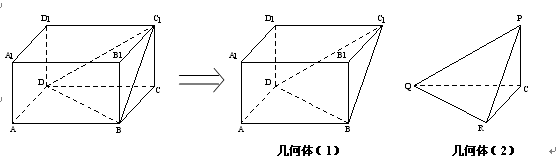
(I)设几何体(1)、几何体(2)的体积分为是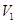 、
、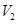 ,求
,求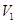 与
与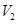 的比值
的比值
(II)在几何体(2)中,求二面角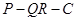 的正切值
的正切值
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
三棱锥P?ABC中,PA⊥平面ABC,AB⊥BC。
(1)证明:平面PAB⊥平面PBC;
(2)若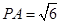 ,
,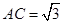 ,PB与底面ABC成60°角,
,PB与底面ABC成60°角,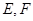 分别是
分别是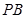 与
与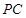 的中点,
的中点,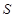 是线段
是线段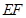 上任意一动点(可与端点重合),求多面体
上任意一动点(可与端点重合),求多面体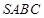 的体积。
的体积。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
有一个倒圆锥形容器,它的轴截面是一个正三角形,在容器内放一个半径为r的铁球,并注入水,使水面与球正好相切,然后将球取出,求这时容器中水的深度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com