Question

10．有下列命题：
①若函数f（x）=3sin（ωx+φ）对于任意的x都有f（$\frac{π}{6}$+x）=-f（$\frac{π}{6}$-x），则f（$\frac{π}{6}$）=0；
②正切函数在定义域上单调递增；
③曲线g（x）=x²与曲线f（x）=2^x有三个公共点；
④若$\overrightarrow{a}$∥$\overrightarrow{b}$，则有且只有一个实数λ，使$\overrightarrow{b}$=λ$\overrightarrow{a}$；
⑤已知函数f（x）=$\left\{\begin{array}{l}{sin（\frac{π}{2}x）-1，x＜0}\\{lo{g}_{a}x（a＞0，a≠1），x＞0}\end{array}\right.$的图象上关于y轴对称的点至少有3对，则实数a的取值范围是（0，$\frac{\sqrt{5}}{5}$）．
其中正确命题的序号是①③⑤．

Answer 1

分析 运用正弦函数的对称性，即可判断①；由正切函数的单调区间即可判断②；
令h（x）=x²-2^x，可得h（2）=h（4）=0，再由零点存在定理，可得h（x）在x＜0有一个零点，即可判断③；
运用向量共线定理，即可判断④；画出f（x）关于y轴对称的图象，设g（x）=-sin（$\frac{π}{2}$x）-1，x＞0，
通过图象观察，可得0＜a＜1且满足g（5）＜f（5），解不等式即可判断⑤．

解答 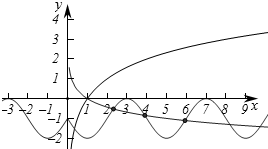解：对于①，若函数f（x）=3sin（ωx+φ）对于任意的x都有f（$\frac{π}{6}$+x）=-f（$\frac{π}{6}$-x），
即有f（x）的图象关于点（$\frac{π}{6}$，0）对称，则f（$\frac{π}{6}$）=0，故①正确；
对于②，由正切函数的性质，可得正切函数在（kπ-$\frac{π}{2}$，kπ+$\frac{π}{2}$），k∈Z单调递增，故②错误；
对于③，令h（x）=x²-2^x，可得h（2）=h（4）=0，h（-1）＞0，h（0）＜0，且h（x）在（-1，0）递减，
即有h（x）在（-1，0）有一个零点，故曲线g（x）=x²与曲线f（x）=2^x有三个公共点正确；
对于④，若$\overrightarrow{a}$∥$\overrightarrow{b}$，（$\overrightarrow{a}$≠$\overrightarrow{0}$），则有且只有一个实数λ，使$\overrightarrow{b}$=λ$\overrightarrow{a}$；若$\overrightarrow{a}$=$\overrightarrow{0}$，则λ有无数个，故④错误；
对于⑤，若x＞0，则-x＜0，
∵x＜0时，f（x）=sin（$\frac{π}{2}$x）-1，
∴f（-x）=sin（-$\frac{π}{2}$x）-1=-sin（$\frac{π}{2}$x）-1，
则若f（x）=sin（$\frac{π}{2}$x）-1，（x＜0）关于y轴对称，
则f（-x）=-sin（$\frac{π}{2}$x）-1=f（x），
即y=-sin（$\frac{π}{2}$x）-1，x＞0，
设g（x）=-sin（$\frac{π}{2}$x）-1，x＞0，
作出函数g（x）的图象，
要使y=-sin（$\frac{π}{2}$x）-1，x＞0与f（x）=log_ax，x＞0的图象至少有3个交点，
则0＜a＜1且满足g（5）＜f（5），即-2＜log_a5，即log_a5＞log_aa^-2，则5＜$\frac{1}{{a}^{2}}$，
解得0＜a＜$\frac{\sqrt{5}}{5}$，故⑤正确．
故答案为：①③⑤．

点评 本题考查三角函数的图象和性质，考查函数的零点的判断和向量共线定理的运用，考查对数函数的图象的性质，属于中档题．