练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】设函数 ． （I）求 的值；
    （II）若f（a）＞f（﹣a），求实数a的取值范围．

    【答案】解：（Ⅰ）f（﹣ ）=log0.5（ ）=2，f（2）=log22=1，∴ =1，
    （Ⅱ）当x＞0时，f（x）=log2x，函数为增函数，
    当x＜0时，f（x）=log0.5（﹣x），函数也为增函数，
    ∵f（a）＞f（﹣a），
    当a＞0时，则log2a＞log0.5a=log2 ，即a＞ ，解得a＞1，
    当a＜0时，则log0.5（﹣a）=log2（﹣a）即log2 ＞log2（﹣a），即﹣ ＞﹣a，解得﹣1＜a＜0
    综上所述实数a的取值范围（﹣1，0）∪（1，+∞）
    【解析】（Ⅰ）根据分段函数的解析，代值计算即可，（Ⅱ）对a进行分类讨论，即可求出a的取值范围．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】随着生活水平的提高，人们对空气质量的要求越来越高，某机构为了解公众对“车辆限行”的态度，随机抽查了50人，并将调查情况进行整理后制成下表：

    （1）规定：年龄在内的为青年人，年龄在内的为中年人，根据以上统计数据填写下面列联表：

    （2）能否在犯错误的概率不超过0.025的前提下，认为赞成“车辆限行”与年龄有关？

    参考公式和数据： ，其中.

    0.100

    0.050

    0.025

    0.010

    2.706

    3.841

    5.024

    6.635

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数存在两个极值点．

    （Ⅰ）求实数a的取值范围；

    （Ⅱ）设和分别是的两个极值点且，证明： ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，其中.

    (Ⅰ) 当a＝－1时，求证： ；

    (Ⅱ) 对任意，存在，使成立，求a的取值范围.

    （其中e是自然对数的底数，e＝2.71828…）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系xOy中，椭圆C的参数方程为（θ为参数），直线l的参数方程为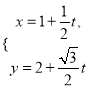（t为参数）．

    （Ⅰ）写出椭圆C的普通方程和直线l的倾斜角；

    （Ⅱ）若点P（1，2），设直线l与椭圆C相交于A，B两点，求|PA|·|PB|的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知f（x）是定义在区间（0，+∞）上的增函数，f（2）=1，且对于任意a，b∈（0，+∞）， 恒成立． （I）求f（8）；
    （II）求不等式 的解集．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数 ．
    （1）求证：f（x）在（0，+∞）上是单调递增函数；
    （2）若f（x）在 上的值域是 ，求a的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，过椭圆： 的左右焦点分别作直线， 交椭圆于与，且.

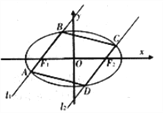
    （1）求证：当直线的斜率与直线的斜率都存在时， 为定值；

    （2）求四边形面积的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示,正三角形ABC所在平面与梯形BCDE所在平面垂直,,=4 ,,F为棱AE的中点.

    (1)求证：平面平面；

    (2)若直线与平面所成角为,求二面角的余弦值.

    查看答案和解析>>

    同步练习册答案