
| A. | 1 | B. | $\sqrt{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\sqrt{3}$ |
分析 利用向量的运算法则和数量积运算,即可得出结论.
解答 解:平行四边形ABCD中,$\overrightarrow{AC}$=$\overrightarrow{AB}$+$\overrightarrow{AD}$,
$\overrightarrow{BE}$=$\overrightarrow{BC}$+$\overrightarrow{CE}$=$\overrightarrow{AD}$-$\frac{1}{2}$$\overrightarrow{AB}$,
∴4=$\overrightarrow{AC}$•$\overrightarrow{BE}$=($\overrightarrow{AB}$+$\overrightarrow{AD}$)•($\overrightarrow{AD}$-$\frac{1}{2}$$\overrightarrow{AB}$)
=${\overrightarrow{AD}}^{2}$+$\frac{1}{2}$$\overrightarrow{AB}$•$\overrightarrow{AD}$-$\frac{1}{2}$${\overrightarrow{AB}}^{2}$,
即4=22+$\frac{1}{2}$×|$\overrightarrow{AB}$|×2×cos60°-$\frac{1}{2}$${|\overrightarrow{AB}|}^{2}$,
又|$\overrightarrow{AB}$|>0,
解得|$\overrightarrow{AB}$|=1.
故选:A.
点评 本题考查了向量的运算法则和数量积运算问题,也考查了一元二次方程的解法问题,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | 18,$\frac{1}{3}$ | B. | 12,$\frac{2}{3}$ | C. | 18,$\frac{2}{3}$ | D. | 12,$\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
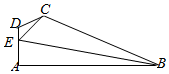 如图,在平面四边形ABCD中,DA⊥AB,DE=2,EC=$\sqrt{7}$,EA=3,∠ADC=$\frac{2π}{3}$,∠BEC=$\frac{π}{2}$.
如图,在平面四边形ABCD中,DA⊥AB,DE=2,EC=$\sqrt{7}$,EA=3,∠ADC=$\frac{2π}{3}$,∠BEC=$\frac{π}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ±$\sqrt{2}$ | B. | ±1 | C. | 1 | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x0>0,不等式x0-1≥lnx0成立 | B. | ?x0>0,不等式x0-1<lnx0成立 | ||
| C. | ?x≤0,不等式x-1≥lnx成立 | D. | ?x>0,不等式x-1<lnx成立 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com