
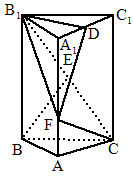
如下图所示,直三棱柱
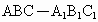 中,底面是以∠ABC为直角的等腰直角三角形,AC=2a,
中,底面是以∠ABC为直角的等腰直角三角形,AC=2a,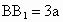 ,D为
,D为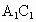 的中点,E为
的中点,E为 的中点.
的中点.
(1)
求直线BE与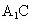 所成的角的余弦值;
所成的角的余弦值;
(2)
在线段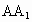 上是否存在点F,使CF⊥平面
上是否存在点F,使CF⊥平面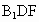 ,若存在,求出AF的长;若不存在,说明理由.
,若存在,求出AF的长;若不存在,说明理由.
科目:高中数学 来源:设计必修二数学北师版 北师版 题型:044
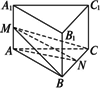
如下图所示,直三棱柱ABC-A1B1C1中,底面为等腰三角形,底边BC长为a,过BC作与底面成![]() 角(0<
角(0<![]() <
<![]() )的平面交AA1于M,若截得的锥体M-ABC的体积为V,求截面△MBC的面积.
)的平面交AA1于M,若截得的锥体M-ABC的体积为V,求截面△MBC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
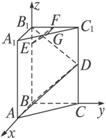
(1)B1D⊥平面ABD;
(2)平面EGF∥平面ABD.
查看答案和解析>>
科目:高中数学 来源: 题型:
如下图所示,直三棱柱A1B1C1―ABC中,C1C=CB=CA=2,AC⊥CB,D,E分别为棱C1C,B1C1的中点。
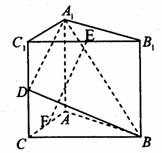
(1)求点B到面A1C1CA的距离;
(2)求二面角B―A1D―A的大小;
(3)在线段AC上是否存在一点F,使得EF⊥平面A1BD?若存在,确定其位置并证明结论;若不存在,说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
如下图所示,直三棱柱A1B1C1―ABC中,C1C=CB=CA=2,AC⊥CB,D,E分别为棱C1C,B1C1的中点。
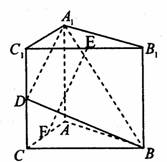
(1)求点B到面A1C1CA的距离;
(2)求二面角B―A1D―A的大小;
(3)在线段AC上是否存在一点F,使得EF⊥平面A1BD?若存在,确定其位置并证明结论;若不存在,说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com