
已知数列{an}的前n项和为Sn,且满足Sn=n2,数列{bn}满足bn=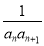 ,Tn为数列{bn}的前n项和.
,Tn为数列{bn}的前n项和.
(1)求数列{an}的通项公式an和Tn;
(2)若对任意的n∈N*,不等式λTn<n+(-1)n恒成立,求实数λ的取值范围.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练13练习卷(解析版) 题型:填空题
已知ABCD-A1B1C1D1为正方体,①( +
+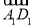 +
+ )2=3
)2=3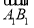 2;②
2;② ·(
·(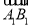 -
-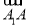 )=0;③向量
)=0;③向量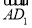 与向量
与向量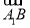 的夹角是60°;④正方体ABCD-A1B1C1D1的体积为|
的夹角是60°;④正方体ABCD-A1B1C1D1的体积为|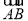 ·
·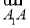 ·
·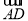 |.其中正确命题的序号是________.
|.其中正确命题的序号是________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷5练习卷(解析版) 题型:解答题
如图,在平面直角坐标系xOy中,椭圆C: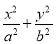 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为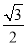 ,以坐标原点为圆心,椭圆C的短半轴长为半径的圆与直线x-y+2=0相切.
,以坐标原点为圆心,椭圆C的短半轴长为半径的圆与直线x-y+2=0相切.
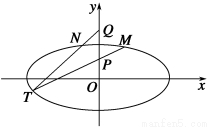
(1)求椭圆C的方程;
(2)已知点P(0,1),Q(0,2),设M,N是椭圆C上关于y轴对称的不同两点,直线PM与QN相交于点T.求证:点T在椭圆C上.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷4练习卷(解析版) 题型:解答题
如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形,O为底面中心,A1O⊥平面ABCD,AB=AA1=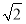 .
.
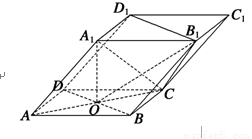
(1)证明:A1C⊥平面BB1D1D;
(2)求平面OCB1与平面BB1D1D的夹角θ的大小.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷4练习卷(解析版) 题型:选择题
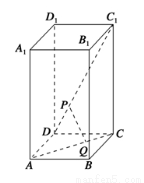
如图,在正四棱柱ABCD-A1B1C1D1中,AA1=2,AB=BC=1,动点P,Q分别在线段C1D,AC上,则线段PQ长度的最小值是( ).
A. B.
B. 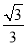 C.
C. 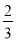 D.
D.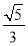
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷3练习卷(解析版) 题型:填空题
已知数列{an}是公差不为0的等差数列,{bn}是等比数列,其中a1=3,b1=1,a2=b2,3a5=b3,若存在常数u,v对任意正整数n都有an=3logubn+v,则u+v=________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷3练习卷(解析版) 题型:选择题
若-9,a,-1成等差数列,-9,m,b,n,-1成等比数列,则ab=( ).
A.15 B.-15 C.±15 D.10
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷2练习卷(解析版) 题型:选择题
已知向量a,b满足|a|=2,|b|=1,且(a+b)⊥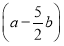 ,则a与b的夹角为( ).
,则a与b的夹角为( ).
A.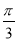 B.
B.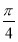 C.
C.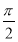 D.
D.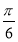
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com