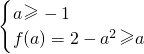Question

设f（x）=x²-2ax+2（a∈R），g（x）=lg^f（x）
（1）当x∈R时，f（x）≥a恒成立，求a的取值范围；
（2）若g（x）的值域为R，求a的取值范围；
（3）当x∈[-1，+∞）时，f（x）≥a恒成立，求a的取值范围．

Answer 1

解：（1）∵x∈R时，有x²-2ax+2-a≥0恒成立，
须△=4a²-4（2-a）≤0，即a²+a-2≤0，所以-2≤a≤1．
a的取值范围-2≤a≤1；
（2）若函数的值域为R，则x²-2ax+2=（x-a）²+2-a²
∴2-a²≤0，∴a≥ 或a≤-．
（3）f（x）=x²-2ax+2=（x-a）²+2-a²
f（x）图象的对称轴为x=a
为使f（x）≥a在[-1，+∞）上恒成立，
只需f（x）在[-1，?+∞）上的最小值比a大或等于a即可
∴①a≤-1时，f（-1）最小，解，解得-3≤a≤-1
②a≥-1时，f（a）最小，解
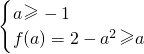
解得-1≤a≤1
综上所述，a的取值范围是：3≤a≤1．
分析：（1）对一切实数x恒成立，转化为二次函数恒为非负，利用根的判别式小于等于0即可．
（2）若函数的值域为R，则x²-2ax+2=（x-a）²+2-a²只须2-a²≤0即可．
（3）区分图象的对称轴与区间[-1，+∞）的关系，根据二次函数在对称轴两边的单调性，求最小值即可解得a的取值范围．
点评：本题考查二次函数在给定区间上的恒成立问题，关键是讨论对称轴与区间的关系，转化为对称轴左右单调性相反，从而确定函数最值，对数函数的性质和二次函数的最值相结合是解题的关键．