练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数f（x）= （a∈R）．
    （1）若不等式f（x）＜1的解集为（﹣1，4），求a的值；
    （2）设a≤0，解关于x的不等式f（x）＞0．

    【答案】
    （1）

    解：∵f（x）＜1，

    ∴ ＜1，∴ ＜0，

    而不等式的解集是（﹣1，4），

    故a﹣1=1，即a=2；


    （2）

    解：①a=0时， ＞0，解得：x＜﹣1，

    ②﹣3＜a＜0时， ＞﹣1，

    ∴ 或 ，

    解得：﹣1＜x＜ ，

    ③a=﹣3时， ＞0，不成立，

    ④a＜﹣3时， ＜﹣1，

    ∴ 或 ，

    解得： ＜a＜﹣1．


    【解析】（1））由f（x）＜1，得到 ＜0，由不等式的解集是（﹣1，4），得到a﹣1=1，解出a的值即可；（2）通过讨论a的范围，解关于x的不等式组，解出即可．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】在棱长为1的正方体ABCDA1B1C1D1中，E为棱BC的中点，点F是棱CD上的动点，试确定点F的位置，使得D1E⊥平面AB1F．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若函数满足:对于任意正数，都有，且，则称函数为“L函数”．

    （1）试判断函数与是否是“L函数”；

    （2）若函数为“L函数”，求实数a的取值范围；

    （3）若函数为“L函数”，且，求证：对任意，都有．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在长方体ABCD﹣A1B1C1D1中，AA1=AD=1，E为CD中点．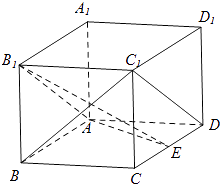

    （1）求证：C1D∥平面AB1E；
    （2）求证：BC1⊥B1E；
    （3）若AB= ，求二面角E﹣AB1﹣B的正切值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为大力提倡“厉行节俭，反对浪费”，某高中通过随机询问100名性别不同的学生是否做到“光盘”行动，得到如表所示联表及附表：

    做不到“光盘”行动

    做到“光盘”行动

    男

    45

    10

    女

    30

    15

    P（K2≥k0）

    0.10

    0.05

    0.025

    k0

    2.706

    3.841

    5.024

    经计算：K2= ≈3.03，参考附表，得到的正确结论是（ ）
    A.有95%的把握认为“该学生能否做到光盘行到与性别有关”
    B.有95%的把握认为“该学生能否做到光盘行到与性别无关”
    C.有90%的把握认为“该学生能否做到光盘行到与性别有关”
    D.有90%的把握认为“该学生能否做到光盘行到与性别无关”

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数f（x）=a2x+ （a，b，c为常数，且a＞0，c＞0）．
    （1）当a=1，b=0时，求证：|f（x）|≥2c；
    （2）当b=1时，如果对任意的x＞1都有f（x）＞a恒成立，求证：a+2c＞1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-4：坐标系与参数方程

    在直角坐标系中，直线的参数方程为（为参数），在极坐标系（与直角坐标系取相同的长度单位，且以原点为极点，以轴正半轴为极轴）中，圆的方程为.

    （1）求圆的直角坐标方程；

    （2）设圆与直线交于点，若点的坐标为，求的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】【2017安徽淮南二模】随着社会发展，淮北市在一天的上下班时段也出现了堵车严重的现象.交通指数是交通拥堵指数的简称，是综合反映道路网畅通或拥堵的概念．记交通指数为T，其范围为[0，10]，分别有5个级别：T∈[0，2)畅通；T∈[2，4)基本畅通；T∈[4，6)轻度拥堵；T∈[6，8)中度拥堵；T∈[8，10]严重拥堵．早高峰时段(T≥3 )，从淮北市交通指挥中心随机选取了一至四马路之间50个交通路段，依据交通指数数据绘制的直方图如图所示：

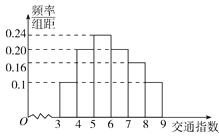
    (I)据此直方图估算交通指数T∈[4，8)时的中位数和平均数；

    (II)据此直方图求出早高峰一至四马路之间的3个路段至少有2个严重拥堵的概率是多少？

    (III)某人上班路上所用时间若畅通时为20分钟，基本畅通为30分钟，轻度拥堵为35分钟，中度拥堵为45分钟，严重拥堵为60分钟，求此人用时间的数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知直四棱柱ABCD﹣A1B1C1D1的底面ABCD为菱形，且∠BCD=60°，P为AD1的中点，Q为BC的中点

    （1）求证：PQ∥平面D1DCC1；
    （2）求证：DQ⊥平面B1BCC1 ．

    查看答案和解析>>

    同步练习册答案