
【题目】已知函数![]() .
.
(1)若函数![]() 有且只有一个零点,求实数
有且只有一个零点,求实数![]() 的值;
的值;
(2)证明:当![]() 时,
时, ![]() .
.
科目:高中数学 来源: 题型:
【题目】如图,在海岸线![]() 一侧
一侧![]() 处有一个美丽的小岛,某旅游公司为方便游客,在
处有一个美丽的小岛,某旅游公司为方便游客,在![]() 上设立了
上设立了![]() 两个报名点,满足
两个报名点,满足![]() 中任意两点间的距离为
中任意两点间的距离为![]() .公司拟按以下思路运作:先将
.公司拟按以下思路运作:先将![]() 两处游客分别乘车集中到
两处游客分别乘车集中到![]() 之间的中转点
之间的中转点![]() 处(点
处(点![]() 异于
异于![]() 两点),然后乘同一艘轮游轮前往
两点),然后乘同一艘轮游轮前往![]() 岛.据统计,每批游客
岛.据统计,每批游客![]() 处需发车2辆,
处需发车2辆, ![]() 处需发车4辆,每辆汽车每千米耗费
处需发车4辆,每辆汽车每千米耗费![]() 元,游轮每千米耗费
元,游轮每千米耗费![]() 元.(其中
元.(其中![]() 是正常数)设∠
是正常数)设∠![]() ,每批游客从各自报名点到
,每批游客从各自报名点到![]() 岛所需运输成本为
岛所需运输成本为![]() 元.
元.
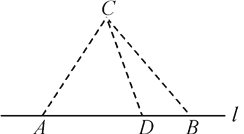
(1) 写出![]() 关于
关于![]() 的函数表达式,并指出
的函数表达式,并指出![]() 的取值范围;
的取值范围;
(2) 问:中转点![]() 距离
距离![]() 处多远时,
处多远时, ![]() 最小?
最小?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线E的中心在坐标原点,离心率为2,E的右焦点与抛物线C:y2=8x的焦点重合,A、B是C的准线与E的两个交点,则|AB|=( )
A.3
B.6
C.9
D.12
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,
且∠DAB=90°,∠ABC=45°,CB= ![]() ,AB=2,PA=1
,AB=2,PA=1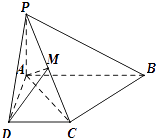
(1)求证:AB∥平面PCD;
(2)求证:BC⊥平面PAC;
(3)若M是PC的中点,求三棱锥C﹣MAD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系中,曲线![]() 的普通方程为
的普通方程为![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系.
轴正半轴为极轴,建立极坐标系.
(1)求曲线![]() 、
、![]() 的极坐标方程;
的极坐标方程;
(2)求曲线![]() 与
与![]() 交点的极坐标,其中
交点的极坐标,其中![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义域为(0,+∞)的单调函数,若对任意的x∈(0,+∞),都有f[f(x)﹣ ![]() ]=2,则f(2016)=( )
]=2,则f(2016)=( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com