
【题目】已知关于x的方程x2﹣2alnx﹣2ax=0有唯一解,则实数a的值为( )
A.1
B.![]()
C.![]()
D.![]()
【答案】B
【解析】解:由选项知a>0,
设g(x)=x2﹣2alnx﹣2ax,(x>0),
若方程x2﹣2alnx﹣2ax=0有唯一解,
即g(x)=0有唯一解,
则g′(x)=2x﹣ ![]() ﹣2a=
﹣2a= ![]() ,
,
令g′(x)=0,可得x2﹣ax﹣a=0,
∵a>0,x>0,∴x1= ![]() (另一根舍去),
(另一根舍去),
当x∈(0,x1)时,g′(x)<0,g(x)在(0,x1)上是单调递减函数;
当x∈(x1 , +∞)时,g′(x)>0,g(x)在(x1 , +∞)上是单调递增函数,
∴当x=x2时,g′(x1)=0,g(x)min=g(x1),
∵g(x)=0有唯一解,
∴g(x1)=0,
∴  ,
,
∴  ,
,
∴2alnx1+ax1﹣a=0
∵a>0,
∴2lnx1+x1﹣1=0,
设函数h(x)=2lnx+x﹣1,
∵x>0时,h(x)是增函数,
∴h(x)=0至多有一解,
∵h(1)=0,
∴方程2lnx1+x1﹣1=0的解为x1=1,
即x1= ![]() =1,
=1,
∴ ![]() ,
,
∴当a>0,方程f(x)=2ax有唯一解时a的值为 ![]() .
.
故选:B.
构造函数g(x)=x2﹣2alnx﹣2ax,将方程有唯一解,转化为g(x)=0有唯一解,即可求得a的值.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:
【题目】加工爆米花时,爆开且不糊的粒数占加工总粒数的百分比称为“可食用率”,在特定条件下,可食用率p与加工时间t(单位:分钟)满足函数关系p=at2+bt+c(a,b,c是常数),如图记录了三次实验的数据,根据上述函数模型和实验数据,可以得到最佳加工时间为( ) 
A.3.50分钟
B.3.75分钟
C.4.00分钟
D.4.25分钟
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|(x+3)(x﹣6)≥0},B={x| ![]() <0}.
<0}.
(1)求A∩RB;
(2)已知E={x|2a<x<a+1}(a∈R),若EB,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知y=f(x)是定义在R上的奇函数,且x>0时,f(x)=1+( ![]() )x
)x
(1)求函数f(x)的解析式;
(2)画出函数f(x)的草图; 
(3)利用图象直接写出函数f(x)的单调区间及值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若变量x,y满足约束条件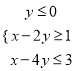 ,则z=3x+5y的取值范围是( )
,则z=3x+5y的取值范围是( )
A. [3,+∞) B. [﹣8,3] C. (﹣∞,9] D. [﹣8,9]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图的程序框图表示求式子1×3×7×15×31×63的值,则判断框内可以填的条件为( ) 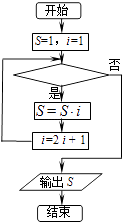
A.i≤31?
B.i≤63?
C.i≥63?
D.i≤127?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x| ![]() ≤(
≤( ![]() )x﹣1≤9},集合B={x|log2x<3},集合C={x|x2﹣(2a+1)x+a2+a≤0},U=R
)x﹣1≤9},集合B={x|log2x<3},集合C={x|x2﹣(2a+1)x+a2+a≤0},U=R
(1)求集合A∩B,(UB)∪A;
(2)若A∪C=A,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com