解:(I)若

,则 sinx(sinx-2cosx)=cos
2x,…(1分)
即-sin2x=cos2x,∴tan2x=-1.-----(2分)
又∵-

<x<

,∴-

<2 x<π,
∴2x=-

,或 2x=

,即 x=-

或 x=

.--------(4分)
(II)∴f(x)=

=2sinxcosx-2cos
2x=sin2x-cos2x=

sin(2x-

)-1,…(7分)
令 2kπ+

≤2x-

≤2kπ+

,k∈z,解得kπ+

≤x≤kπ+

.
又
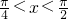
,
∴f(x)的单调减区间时(-

,-

)、(

,

).…(11分)
(Ⅲ)能,将函数f(x)的图象向上平移1个单位,再向左平移
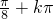
( k∈N) 个单位,或向右平移
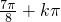
( k∈N) 个单位,
即得函数 g(x)=

sin2x的图象,而 g(x)为奇函数.…(13分)
分析:(I)利用两个向量共线的性质求得 tan2x=-1,再由-

<x<

求得x的值.
(II)利用两个向量的数量积公式 化简 f(x)的解析式为

sin(2x-

)-1,令 2kπ+

≤2x-

≤2kπ+

,k∈z,求得x的范围,即可求得函数的减区间.
(Ⅲ)将函数f(x)的图象向上平移1个单位,再向左平移
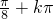
( k∈N) 个单位,或向右平移
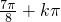
( k∈N) 个单位即可.
点评:本题主要考查两个向量共线的性质、两个向量的数量积公式,两角和差的正弦公式,函数y=Asin(ωx+∅)的图象变换规律,属于中档题.

 =(sinx,cosx),
=(sinx,cosx), =(cosx,-2cosx),-
=(cosx,-2cosx),-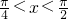 .
. ∥
∥ ,求x;
,求x; •
• ,求f(x)的单调减区间;
,求f(x)的单调减区间; ,则 sinx(sinx-2cosx)=cos2x,…(1分)
,则 sinx(sinx-2cosx)=cos2x,…(1分) <x<
<x< ,∴-
,∴- <2 x<π,
<2 x<π, ,或 2x=
,或 2x= ,即 x=-
,即 x=- 或 x=
或 x= .--------(4分)
.--------(4分) =2sinxcosx-2cos2x=sin2x-cos2x=
=2sinxcosx-2cos2x=sin2x-cos2x= sin(2x-
sin(2x- )-1,…(7分)
)-1,…(7分) ≤2x-
≤2x- ≤2kπ+
≤2kπ+ ,k∈z,解得kπ+
,k∈z,解得kπ+ ≤x≤kπ+
≤x≤kπ+ .
.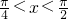 ,
, ,-
,- )、(
)、(  ,
, ).…(11分)
).…(11分)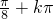 ( k∈N) 个单位,或向右平移
( k∈N) 个单位,或向右平移 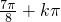 ( k∈N) 个单位,
( k∈N) 个单位, sin2x的图象,而 g(x)为奇函数.…(13分)
sin2x的图象,而 g(x)为奇函数.…(13分) <x<
<x< 求得x的值.
求得x的值. sin(2x-
sin(2x- )-1,令 2kπ+
)-1,令 2kπ+ ≤2x-
≤2x- ≤2kπ+
≤2kπ+ ,k∈z,求得x的范围,即可求得函数的减区间.
,k∈z,求得x的范围,即可求得函数的减区间.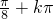 ( k∈N) 个单位,或向右平移
( k∈N) 个单位,或向右平移 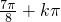 ( k∈N) 个单位即可.
( k∈N) 个单位即可.
