
【题目】![]() 年下学期某市教育局对某校高三文科数学进行教学调研,从该校文科生中随机抽取
年下学期某市教育局对某校高三文科数学进行教学调研,从该校文科生中随机抽取![]() 名学生的数学成绩进行统计,将他们的成绩分成六段
名学生的数学成绩进行统计,将他们的成绩分成六段![]() 后得到如图所示的频率分布直方图.
后得到如图所示的频率分布直方图.

(1)求这40名学生中数学成绩不低于120分的学生人数;
(2)若从数学成绩![]() 内的学生中任意抽取2人,求成绩在
内的学生中任意抽取2人,求成绩在![]() 中至少有一人的概率.
中至少有一人的概率.
【答案】(1)14;(2)![]() 。
。
【解析】
试题分析:(1)根据频率分布直方图可知,每个小长方形的面积等于该组相应的频率,所有小长方形面积和等于频率之和,等于1。成绩不低于120分的为最后两组,这两组的频率和为(0.025+0.010)×10=0.35,所以40名学生中,根据频率分布直方图估计,成绩不低于120分的人数为40×0.35=14人,本问考查频率分布直方图,属于对基础知识的考查。(2)根据频率分布直方图可知,成绩在[80,100)内的频率为(0.005+0.010)×10=0.15,人数为40×0.15=6人,期中成绩在[80,90)内的频率为0.010×10=0.1,人数为40×0.1=4人,设这四人编号为a,b,c,d,其余两人编号为e,f,从6人中任选2人,可以写出所有基本事件![]() ,
,![]() 共
共![]() 种.设成绩在
种.设成绩在![]() 的学生至少有一人为基本事件A,则事件A包含的基本事件如下:
的学生至少有一人为基本事件A,则事件A包含的基本事件如下:![]() 共9种,则根据古典概型概率公式,事件A的概率为
共9种,则根据古典概型概率公式,事件A的概率为![]() 。
。
试题解析:(1)(0.025+0.010)×10=0.35,人数为40×0.35=14人
(2)从图中知,成绩在![]() 的人数为
的人数为![]() (人), 成绩在
(人), 成绩在![]() 的人数为
的人数为![]() (人), 设成绩在
(人), 设成绩在![]() 的学生记为
的学生记为![]() ,成绩在
,成绩在![]() 的学生记为
的学生记为![]() .则从成绩在
.则从成绩在![]() 内的学生中任取
内的学生中任取![]() 人组成的基本事件有
人组成的基本事件有![]() ,
,![]() 共
共![]() 种.其中成绩在
种.其中成绩在![]() 的学生至少有一人的基本事件有
的学生至少有一人的基本事件有![]() 共9种.
共9种.
![]() 成绩在
成绩在![]() 的学生至少有一人的概率为
的学生至少有一人的概率为![]() .
.


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:高中数学 来源: 题型:
【题目】下列各组几何体中,都是多面体的一组是( )
A. 三棱柱、四棱台、球、圆锥 B. 三棱柱、四棱台、正方体、圆台
C. 三棱柱、四棱台、正方体、六棱锥 D. 圆锥、圆台、球、半球
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列关于四种命题的真假判断正确的是( )
A. 原命题与其逆否命题的真值相同 B. 原命题与其逆命题的真值相同
C. 原命题与其否命题的真值相同 D. 原命题的逆命题与否命题的真值相反
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() ,直线
,直线![]() ,设圆
,设圆![]() 的半径为
的半径为![]() ,圆心在
,圆心在![]() 上.
上.
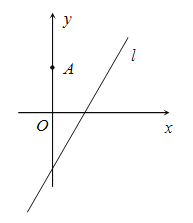
(Ⅰ)若圆心![]() 也在直线
也在直线![]() 上,过点
上,过点![]() 作圆
作圆![]() 的切线,求切线的方程;
的切线,求切线的方程;
(Ⅱ)若圆![]() 上存在点
上存在点![]() ,使
,使![]() ,求圆心
,求圆心![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 是定义域为R的奇函数.
是定义域为R的奇函数.
(1)求![]() 的值;
的值;
(2)若![]() ,试判断
,试判断![]() 的单调性(不需证明),并求使不等式
的单调性(不需证明),并求使不等式![]() 恒成立的t的取值范围;
恒成立的t的取值范围;
(3)若![]() ,
,![]() ,求
,求![]() 在
在![]() 上的最小值.
上的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,过点
中,过点![]() 的直线
的直线![]() 的倾斜角为45°,以坐标原点为极点,
的倾斜角为45°,以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 和曲线
和曲线![]() 的交点为点
的交点为点![]() .
.
(1)求直线![]() 的参数方程;
的参数方程;
(2)求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com