
下列说法:
①将一组数据中的每个数据都加上或减去同一个常数后,方差恒不变;
②设有一个回归方程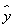 =3-5x,变量x增加一个单位时,y平均增加5个单位;
=3-5x,变量x增加一个单位时,y平均增加5个单位;
③线性回归方程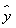 =
=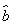 x+
x+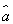 必过(
必过(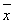 ,
,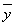 );
);
④在一个2×2列联表中,由计算得K2=13.079,则有99%的把握确认这两个变量间有关系.
其中错误的个数是( )
本题可以参考独立性检验临界值表:
P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
A.0 B.1 C.2 D.3
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)仿真模拟卷1练习卷(解析版) 题型:填空题
向量a,b,c满足:|a|=1,|b|=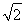 ,b在a方向上的投影为
,b在a方向上的投影为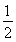 ,(a-c)·(b-c)=0,则|c|的最大值是________.
,(a-c)·(b-c)=0,则|c|的最大值是________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷6练习卷(解析版) 题型:解答题
某车间将10名技工平均分成甲、乙两组加工某种零件,在单位时间内每个技工加工的合格零件数如下表:
| 1号 | 2号 | 3号 | 4号 | 5号 |
甲组 | 4 | 5 | x | 9 | 10 |
乙组 | 5 | 6 | 7 | y | 9 |
(1)已知两组技工在单位时间内加工的合格零件平均数为7,分别求出甲、乙两组技工在单位时间内加工的合格零件的方差,并由此分析两组技工的加工水平;
(2)质检部门从该车间甲、乙两组中各随机抽取一名技工,对其加工的零件进行检测,若2人加工的合格零件个数之和超过14,则称该车间“质量合格”,求该车间“质量合格”的概率.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷6练习卷(解析版) 题型:填空题
右图是根据部分城市某年6月份的平均气温(单位:℃)数据得到的样本频率分布直方图,其中平均气温的范围是[20.5,26.5],样本数据的分组为[20.5,21.5),[21.5,22.5),[22.5,23.5),[23.5,24.5),[24.5,25.5),[25.5,26.5].已知样本中平均气温低于22.5 ℃的城市个数为11,则样本中平均气温不低于25.5 ℃的城市个数为________.
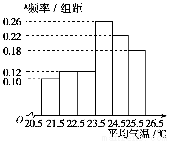
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷6练习卷(解析版) 题型:选择题
从1,2,3,4中任取2个不同的数,则取出的2个数之差的绝对值为2的概率是( )
A.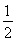 B.
B.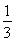 C.
C.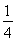 D.
D.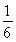
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷5练习卷(解析版) 题型:解答题
已知圆C经过点A(-2,0),B(0,2),且圆心C在直线y=x上,又直线l:y=kx+1与圆C相交于P、Q两点.
(1)求圆C的方程;
(2)若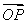 ·
·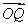 =-2,求实数k的值.
=-2,求实数k的值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷4练习卷(解析版) 题型:解答题
如图,多面体ABC-A1B1C1中,三角形ABC是边长为4的正三角形,AA1∥BB1∥CC1,AA1⊥平面ABC,AA1=BB1=2CC1=4.
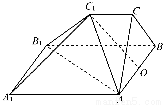
(1)若O是AB的中点,求证:OC1⊥A1B1;
(2)在线段AB1上是否存在一点D,使得CD∥平面A1B1C1,若存在,确定点D的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷2练习卷(解析版) 题型:解答题
已知函数f(x)=2sin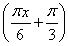 (0≤x≤5),点A、B分别是函数y=f(x)图象上的最高点和最低点.
(0≤x≤5),点A、B分别是函数y=f(x)图象上的最高点和最低点.
(1)求点A、B的坐标以及 ·
·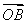 的值;
的值;
(2)设点A、B分别在角α、β的终边上,求tan(α-2β)的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com