
| A. | y2-x2=1(y<0) | B. | (y+2)2+x2=1 | C. | ${x^2}+\frac{y^2}{4}=1(y<0)$ | D. | x2=-y-1 |
分析 设抛物线的弦AB与圆x2+y2=1切于点M(x0,y0),则x02+y02=1,过M点的圆的切线方程为x0x+y0y=1.联立抛物线方程后,根据△>0,可得y0的范围,进而结合-1≤y0≤1且y0<0,可得y0的范围.设出A,B的坐标,由韦达定理可得x1+x2的关系式①,x1x2的关系式②.求出AP,BP的方程,进而可得M的坐标,代入圆的方程可得P点轨迹方程;
解答 解:设抛物线的弦AB与圆x2+y2=1切于点M(x0,y0),
则x02+y02=1,过M点的圆的切线方程为x0x+y0y=1.
由$\left\{\begin{array}{l}{{x}_{0}x+{y}_{0}y=1}\\{{x}^{2}=2y}\end{array}\right.$得$\frac{1}{2}$y0x2+x0x-1=0.(*)
由△=x02+2y0=-y02+2y0+1>0,得1-$\sqrt{2}$<y0<1+$\sqrt{2}$.
令A(x1,$\frac{1}{2}$x12),B(x2,$\frac{1}{2}$x22),知x1、x2是方程(*)的两个实根,
由根与系数的关系,
得x1+x2=-$\frac{{2x}_{0}}{{y}_{0}}$①,x1x2=-$\frac{2}{{y}_{0}}$②.
过A点的抛物线的切线AP的方程为y-$\frac{1}{2}$x12=x1(x-x1),即y=x1x-$\frac{1}{2}$x12.③
同理,BP的方程为y=x2x-$\frac{1}{2}$x22.④
联立①②③④,解得$\left\{\begin{array}{l}{x=\frac{{x}_{0}}{{y}_{0}}}\\{y=-\frac{1}{{y}_{0}}}\end{array}\right.$,
∴$\left\{\begin{array}{l}{{x}_{0}=-\frac{x}{y}}\\{{y}_{0}=-\frac{1}{y}}\end{array}\right.$,
代入x02+y02=1得($-\frac{x}{y}$)2+(-$\frac{1}{y}$)2=1,
整理,得y2-x2=1(x∈R,-y<0),这就是点P的轨迹方程.
故选:A.
点评 本题考查的知识点是抛物线的简单性质,直线与圆锥曲线的关系,综合性强,运算量大,转化困难,难度较大,属于难题.-


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
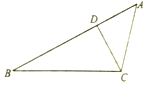 如图,在△ABC中,∠B=30°,AC=2$\sqrt{5}$,D是边AB上一点.
如图,在△ABC中,∠B=30°,AC=2$\sqrt{5}$,D是边AB上一点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | $\sqrt{6}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com