
【题目】在四棱锥P﹣ABCD中,PC⊥底面ABCD,M是PD的中点,AC⊥AD,BA⊥BC,PC=AC=2BC,∠ACD=∠ACB. 
(1)求证:PA⊥CM;
(2)求二面角M﹣AC﹣P的余弦值.
【答案】
(1)证明:取PA的中点N,连接MN,NC,
∵MN为△PAD的中位线,∴MN∥AD,
∵PC⊥底面ABCD,∴PC⊥AD,
又∵AC⊥AD,PC∩AD=C,∴AD⊥平面PAC,
∴AD⊥PA,则MN⊥PA,
∵PC=AC,N为PA的中点,∴CN⊥PA,
∵MN∩NC=N,∴PA⊥平面MNC,
又∵CM平面MNC,∴PA⊥CM
(2)解:设PC=AC=1,则BC= ![]() ,
,
∵BA⊥BC,∴cos ![]() ,
,
∴∠ACD=∠ACB=60°,
又∵AC⊥CD,∴CD=2.
以B为坐标原点,以BA、CB所在直线分别为x、y轴,以过B点和PC平行的直线为z轴距离如图所示坐标系.
则A( ![]() ,0,0),C(0,﹣
,0,0),C(0,﹣ ![]() ,0),D(
,0),D( ![]() ,﹣
,﹣ ![]() ,0),P(0,﹣
,0),P(0,﹣ ![]() ,1),
,1),
∴M( ![]() ,﹣1,
,﹣1, ![]() ).
).
 ,
,  .
.
∵DA⊥平面PAC,
∴  是平面PAC的一个法向量.
是平面PAC的一个法向量.
设 ![]() 是平面ACM的一个法向量,
是平面ACM的一个法向量,
则 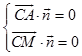 ,即
,即  ,令x=1,得
,令x=1,得 ![]() .
.
∴|cos< ![]() >|=|
>|=|  |=|
|=|  |=
|= ![]() .
.
由图可知,二面角M﹣AC﹣P为锐角,
∴二面角M﹣AC﹣P的余弦值为 ![]() .
.

【解析】(1)取PA的中点N,连接MN,NC,由三角形中位线定理可得MN∥AD,由PC⊥底面ABCD,得PC⊥AD,结合AC⊥AD,可得AD⊥平面PAC,进一步得到MN⊥PA,再由等腰三角形的性质可知CN⊥PA,由线面垂直的判定得到PA⊥平面MNC,则有PA⊥CM;(2)设PC=AC=1,解三角形可得CD=2.以B为坐标原点,以BA、CB所在直线分别为x、y轴,以过B点和PC平行的直线为z轴距离如图所示坐标系.求得A,C,D,P的坐标,进一步求出平面PAC与平面ACM的一个法向量,利用两法向量所成角的余弦值可得二面角M﹣AC﹣P的余弦值.
【考点精析】解答此题的关键在于理解空间中直线与直线之间的位置关系的相关知识,掌握相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点.


科目:高中数学 来源: 题型:
【题目】如图所示茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单位:分),已知甲组数据的中位数为17,乙组数据的平均数为17.4,则x、y的值分别为( ) 
A.7、8
B.5、7
C.8、5
D.7、7
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等边三角形PAB的边长为4,四边形ABCD为正方形,平面PAB⊥平面ABCD,E,F,G,H分别是线段AB,CD,PD,PC上的点.
(1)如图①,若G为线段PD的中点,BE=DF=1,证明:PB∥平面EFG; 
(2)如图②,若E,F分别是线段AB,CD的中点,DG=3GP,GH= ![]() HP,求二面角H﹣EF﹣G的余弦值.
HP,求二面角H﹣EF﹣G的余弦值. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在几何体ABCDQP中,AD⊥平面ABPQ,AB⊥AQ,AB∥CD∥PQ,CD=AD=AQ=PQ= ![]() AB.
AB. 
(1)证明:平面APD⊥平面BDP;
(2)求二面角A﹣BP﹣C的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=  的图象与函数g(x)=log2(x+a)(a∈R)的图象恰有一个交点,则实数a的取值范围是( )
的图象与函数g(x)=log2(x+a)(a∈R)的图象恰有一个交点,则实数a的取值范围是( )
A.a>1
B.a≤﹣ ![]()
C.a≥1或a<﹣ ![]()
D.a>1或a≤﹣ ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C顶点在原点,焦点在y轴上,抛物线C上一点Q(a,2)到焦点的距离为3,线段AB的两端点A(x1 , y1)、B(x2 , y2)在抛物线C上.
(1)求抛物线C的方程;
(2)若y轴上存在一点M(0,m)(m>0),使线段AB经过点M时,以AB为直径的圆经过原点,求m的值;
(3)在抛物线C上存在点D(x3 , y3),满足x3<x1<x2 , 若△ABD是以角A为直角的等腰直角三角形,求△ABD面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,菱ABCD与四边形BDEF相交于BD,∠ABC=120°,BF⊥平面ABCD,DE∥BF,BF=2DE,AF⊥FC,M为CF的中点,AC∩BD=G. 
(I)求证:GM∥平面CDE;
(II)求直线AM与平面ACE成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com