
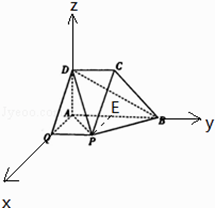
【题目】如图,在几何体ABCDQP中,AD⊥平面ABPQ,AB⊥AQ,AB∥CD∥PQ,CD=AD=AQ=PQ= ![]() AB.
AB. 
(1)证明:平面APD⊥平面BDP;
(2)求二面角A﹣BP﹣C的正弦值.
【答案】
(1)证明:取AB中点E,连结PE,
∵AD⊥平面ABPQ,AB⊥AQ,AB∥CD∥PQ,设CD=AD=AQ=PQ= ![]() AB=1.
AB=1.
∴PB⊥AD,PE=1,且PE⊥AB,
∴AP=PB= ![]() =
= ![]() ,
,
∴AP2+BP2=AB2,∴AP⊥BP,
∵AD∩AP=A,∴PB⊥平面APD,
∵PB平面BDP,∴平面APD⊥平面BDP
(2)解:以A为原点,AQ为x轴,AB为y轴,AD为z轴,
建立空间直角坐标系,
则P(1,1,0),B(0,2,0),C(0,1,1),
![]() =(1,﹣1,0),
=(1,﹣1,0), ![]() =(0,﹣1,1),
=(0,﹣1,1),
设平面BPC的法向量 ![]() =(x,y,z),
=(x,y,z),
则 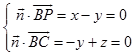 ,取x=1,得
,取x=1,得 ![]() =(1,1,1),
=(1,1,1),
平面ABP的法向量 ![]() =(0,0,1),
=(0,0,1),
设二面角A﹣BP﹣C的平面角为θ,
则cosθ= ![]() =
= ![]() ,
,
∴sinθ= 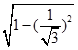 =
= ![]() .
.
∴二面角A﹣BP﹣C的正弦值为 ![]() .
.
【解析】(1)取AB中点E,连结PE,推导出PE⊥AB,AP⊥BP,从而PB⊥平面APD,由此能证明平面APD⊥平面BDP.(2)以A为原点,AQ为x轴,AB为y轴,AD为z轴,建立空间直角坐标系,利用向量法能求出二面角A﹣BP﹣C的正弦值.
【考点精析】本题主要考查了平面与平面垂直的判定的相关知识点,需要掌握一个平面过另一个平面的垂线,则这两个平面垂直才能正确解答此题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,侧面ACC1A1⊥底面ABC,∠A1AC=60°,AC=2AA1=4,点D,E分别是AA1 , BC的中点. 
(1)证明:DE∥平面A1B1C;
(2)若AB=2,∠BAC=60°,求直线DE与平面ABB1A1所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣2|+|x+4|,g(x)=x2+4x+3.
(1)求不等式f(x)≥g(x)的解集;
(2)若f(x)≥|1﹣5a|恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y2=﹣2px(p>0)的焦点F与双曲线x2﹣8y2=8的左焦点重合,点A在抛物线上,且|AF|=6,若P是抛物线准线上一动点,则|PO|+|PA|的最小值为( )
A.3 ![]()
B.4 ![]()
C.3 ![]()
D.3 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() (x>0),m∈R.
(x>0),m∈R.
(1)若函数f(x)有零点,求实数m的取值范围;
(2)若函数f(x)的图象在点(1,f(x))处的切线的斜率为 ![]() ,且函数f(x)的最大值为M,求证:1<M<
,且函数f(x)的最大值为M,求证:1<M< ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,PC⊥底面ABCD,M是PD的中点,AC⊥AD,BA⊥BC,PC=AC=2BC,∠ACD=∠ACB. 
(1)求证:PA⊥CM;
(2)求二面角M﹣AC﹣P的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
如图,在四棱锥P—ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AP=AB,BP=BC=2,E,F分别是PB,PC的中点.
(Ⅰ)证明:EF∥平面PAD;
(Ⅱ)求三棱锥E—ABC的体积V.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两支排球队进行比赛,先胜3局者获得比赛的胜利,比赛随即结束.除第五局甲队获胜的概率是 ![]() ,其余每局比赛甲队获胜的概率都是
,其余每局比赛甲队获胜的概率都是 ![]() .设各局比赛结果相互独立.
.设各局比赛结果相互独立.
(1)分别求甲队3:0,3:1,3:2胜利的概率;
(2)若比赛结果3:0或3:1,则胜利方得3分,对方得0分;若比赛结果为3:2,则胜利方得2分,对方得1分,求乙队得分X的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com