
【题目】甲乙两支排球队进行比赛,先胜3局者获得比赛的胜利,比赛随即结束.除第五局甲队获胜的概率是 ![]() ,其余每局比赛甲队获胜的概率都是
,其余每局比赛甲队获胜的概率都是 ![]() .设各局比赛结果相互独立.
.设各局比赛结果相互独立.
(1)分别求甲队3:0,3:1,3:2胜利的概率;
(2)若比赛结果3:0或3:1,则胜利方得3分,对方得0分;若比赛结果为3:2,则胜利方得2分,对方得1分,求乙队得分X的分布列及数学期望.
【答案】
(1)解:甲队获胜有三种情形,其每种情形的最后一局肯定是甲队胜
①3:0,概率为P1=( ![]() )3=
)3= ![]() ;
;
②3:1,概率为P2=C ![]() (
( ![]() )2×(1﹣
)2×(1﹣ ![]() )×
)× ![]() =
= ![]() ;
;
③3:2,概率为P3=C ![]() (
( ![]() )2×(1﹣
)2×(1﹣ ![]() )2×
)2× ![]() =
= ![]()
∴甲队3:0,3:1,3:2胜利的概率: ![]()
(2)解:乙队得分X,则X的取值可能为0,1,2,3.
由(1)知P(X=0)=P1+P2= ![]() ;
;
P(X=1)=P3= ![]() ;
;
P(X=2)=C ![]() (1﹣
(1﹣ ![]() )2×(
)2×( ![]() )2×
)2× ![]() =
= ![]() ;
;
P(X=3)=(1﹣ ![]() )3+C
)3+C ![]() (1﹣
(1﹣ ![]() )2×(
)2×( ![]() )×
)× ![]() =
= ![]() ;
;
则X的分布列为
X | 3 | 2 | 1 | 0 |
P |
|
|
|
|
E(X)=3× ![]() +2×
+2× ![]() +1×
+1× ![]() +0×
+0× ![]() =
= ![]()
【解析】(1)甲队获胜有三种情形,①3:0,②3:1,③3:2,其每种情形的最后一局肯定是甲队胜,分别求出相应的概率,最后根据互斥事件的概率公式求出甲队获得这次比赛胜利的概率;(2)X的取值可能为0,1,2,3,然后利用相互独立事件的概率乘法公式求出相应的概率,列出分布列,最后根据数学期望公式解之即可.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:高中数学 来源: 题型:
【题目】如图,在几何体ABCDQP中,AD⊥平面ABPQ,AB⊥AQ,AB∥CD∥PQ,CD=AD=AQ=PQ= ![]() AB.
AB. 
(1)证明:平面APD⊥平面BDP;
(2)求二面角A﹣BP﹣C的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(ωx+φ)(ω>0,|φ|≤ ![]() ),x=﹣
),x=﹣ ![]() 为f(x)的零点,x=
为f(x)的零点,x= ![]() 为y=f(x)图象的对称轴,且f(x)在(
为y=f(x)图象的对称轴,且f(x)在( ![]() ,
, ![]() )上单调,则ω的最大值为( )
)上单调,则ω的最大值为( )
A.11
B.9
C.7
D.5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2011年,国际数学协会正式宣布,将每年的3月14日设为国际数学节,来源则是中国古代数学家祖冲之的圆周率.祖冲之,在世界数学史上第一次将圆周率(π)值计算到小数点后的第7位,即3.1415926到3.1415927之间,数列{an}是公差大于0的等差数列,其前三项是“31415926”中连续的三个数,数列{bn}是等比数列,其公比大于1的正整数且前三项是“31415926”中的三个数,且a3=b3 .
(Ⅰ)求数列{an},{bn}的通项公式;
(Ⅱ)cn= 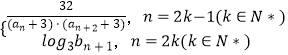 ,求c1+c2+c3+…+c
,求c1+c2+c3+…+c ![]() .(n∈N*)
.(n∈N*)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次试验中,有两个试验数据![]() ,统计的结果如下面的表格1.
,统计的结果如下面的表格1.
(1)在给出的坐标系中画出![]() 的散点图; 并判断正负相关;
的散点图; 并判断正负相关;
(2)填写表格2,然后根据表格2的内容和公式求出![]() 对
对![]() 的回归直线方程
的回归直线方程![]() ,并估计当
,并估计当![]() 为10时
为10时![]() 的值是多少?(公式:
的值是多少?(公式: ,
,![]() )
)
| 1 | 2 | 3 | 4 | 5 |
| 2 | 3 | 4 | 4 | 5 |
表1

表格2
序号 | | | | |
1 | 1 | 2 | ||
2 | 2 | 3 | ||
3 | 3 | 4 | ||
4 | 4 | 4 | ||
5 | 5 | 5 | ||
|
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com