Question

【题目】2011年，国际数学协会正式宣布，将每年的3月14日设为国际数学节，来源则是中国古代数学家祖冲之的圆周率．祖冲之，在世界数学史上第一次将圆周率（π）值计算到小数点后的第7位，即3.1415926到3.1415927之间，数列{an}是公差大于0的等差数列，其前三项是“31415926”中连续的三个数，数列{bn}是等比数列，其公比大于1的正整数且前三项是“31415926”中的三个数，且a3=b3 ．
（Ⅰ）求数列{an}，{bn}的通项公式；
（Ⅱ）cn= 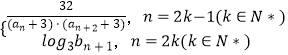，求c1+c2+c3+…+c ．（n∈N*）

Answer 1

【答案】解：（Ⅰ）由题可知a1=1，a2=5，a3=9，

b1=4，b2=6，b3=9，

所以an=1+4（n﹣1）=4n﹣3，bn=4× ；

（Ⅱ）由（I）可知cn= ，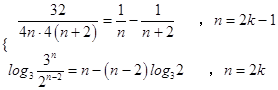

则c1+c3+…+ =1﹣ + ﹣ +…+ ﹣ =1﹣ ，

c2+c4+…+ =（2+4+…+2n）﹣[（2﹣2）+（4﹣2）+（6﹣2）+…+（2n﹣2）]log32

= ﹣[ ﹣2n]log32

=2n﹣1+22n﹣2﹣（22n﹣2﹣2n﹣1）log32，

故所求值为1﹣ +2n﹣1+22n﹣2﹣（22n﹣2﹣2n﹣1）log32

【解析】（Ⅰ）通过题干确定数列{an}、{bn}的前三项，进而可得结论；（Ⅱ）通过（I）可求出cn的表达式，利用裂项相消法可知奇数项的和，利用分组求和法可求出偶数项的和，进而相加即得结论．
【考点精析】掌握数列的前n项和是解答本题的根本，需要知道数列{an}的前n项和sn与通项an的关系．