
【题目】在直角坐标系xOy中,曲线C的参数方程为 ![]() (α为参数)
(α为参数)
(1)求曲线C的普通方程;
(2)在以O为极点,x正半轴为极轴的极坐标系中,直线l方程为 ![]() ρsin(
ρsin( ![]() ﹣θ)+1=0,已知直线l与曲线C相交于A,B两点,求|AB|.
﹣θ)+1=0,已知直线l与曲线C相交于A,B两点,求|AB|.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】2011年,国际数学协会正式宣布,将每年的3月14日设为国际数学节,来源则是中国古代数学家祖冲之的圆周率.祖冲之,在世界数学史上第一次将圆周率(π)值计算到小数点后的第7位,即3.1415926到3.1415927之间,数列{an}是公差大于0的等差数列,其前三项是“31415926”中连续的三个数,数列{bn}是等比数列,其公比大于1的正整数且前三项是“31415926”中的三个数,且a3=b3 .
(Ⅰ)求数列{an},{bn}的通项公式;
(Ⅱ)cn= 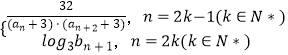 ,求c1+c2+c3+…+c
,求c1+c2+c3+…+c ![]() .(n∈N*)
.(n∈N*)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,且满足csinA=acosC
(1)求角C大小;
(2)求 ![]() sinA﹣cos(B+
sinA﹣cos(B+ ![]() )的最大值,并求取得最大值时角A,B的大小.
)的最大值,并求取得最大值时角A,B的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E: ![]() +
+ ![]() =1(a>b>0)过点
=1(a>b>0)过点 ![]() ,且离心率e为
,且离心率e为 ![]() .
. 
(1)求椭圆E的方程;
(2)设直线x=my﹣1(m∈R)交椭圆E于A,B两点,判断点G ![]() 与以线段AB为直径的圆的位置关系,并说明理由.
与以线段AB为直径的圆的位置关系,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣x2与g(x)=(x﹣2)2﹣ ![]() ﹣m的图象上存在关于(1,0)对称的点,则实数m的取值范围是( )
﹣m的图象上存在关于(1,0)对称的点,则实数m的取值范围是( )
A.(﹣∞,1﹣ln2)
B.(﹣∞,1﹣ln2]
C.(1﹣ln2,+∞)
D.[1﹣ln2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次试验中,有两个试验数据![]() ,统计的结果如下面的表格1.
,统计的结果如下面的表格1.
(1)在给出的坐标系中画出![]() 的散点图; 并判断正负相关;
的散点图; 并判断正负相关;
(2)填写表格2,然后根据表格2的内容和公式求出![]() 对
对![]() 的回归直线方程
的回归直线方程![]() ,并估计当
,并估计当![]() 为10时
为10时![]() 的值是多少?(公式:
的值是多少?(公式: ,
,![]() )
)
| 1 | 2 | 3 | 4 | 5 |
| 2 | 3 | 4 | 4 | 5 |
表1

表格2
序号 | | | | |
1 | 1 | 2 | ||
2 | 2 | 3 | ||
3 | 3 | 4 | ||
4 | 4 | 4 | ||
5 | 5 | 5 | ||
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数y=cos(2x+ ![]() )的图象向左平移
)的图象向左平移 ![]() 个单位后,得到f(x)的图象,则( )
个单位后,得到f(x)的图象,则( )
A.f(x)=﹣sin2x
B.f(x)的图象关于x=﹣ ![]() 对称
对称
C.f( ![]() )=
)= ![]()
D.f(x)的图象关于( ![]() ,0)对称
,0)对称
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com