
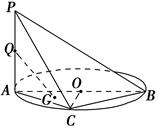
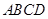 中,点
中,点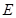 为边
为边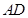 上的点,点
上的点,点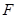 为边
为边 的中点,
的中点,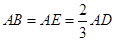 ,现将
,现将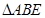 沿
沿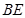 边折至
边折至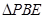 位置,且平面
位置,且平面 平面
平面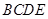 .
.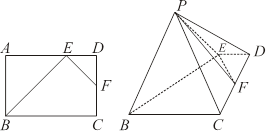
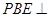 平面
平面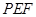 ;
;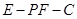 的大小.
的大小.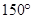 .
.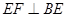 ,折后这个垂直关系没有改变,然后由平面
,折后这个垂直关系没有改变,然后由平面 平面
平面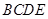 的性质证明
的性质证明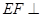 平面
平面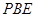 ,最后由面面垂直的判定定理即可证明平面
,最后由面面垂直的判定定理即可证明平面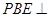 平面
平面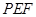 ;(2)为方便计算,不妨设
;(2)为方便计算,不妨设 ,先以
,先以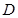 为原点,以
为原点,以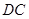 方向为
方向为 轴,以
轴,以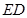 方向为
方向为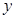 轴,以与平面
轴,以与平面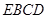 向上的法向量同方向为
向上的法向量同方向为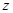 轴,建立空间直角坐标系,写给相应点的坐标,然后分别求出平面
轴,建立空间直角坐标系,写给相应点的坐标,然后分别求出平面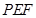 和平面
和平面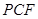 的一个法向量,接着计算出这两个法向量夹角的余弦值,根据二面角的图形与计算出的余弦值,确定二面角的大小即可.
的一个法向量,接着计算出这两个法向量夹角的余弦值,根据二面角的图形与计算出的余弦值,确定二面角的大小即可.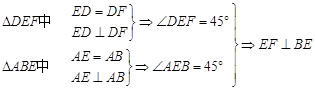 ,这个垂直关系,折后没有改变
,这个垂直关系,折后没有改变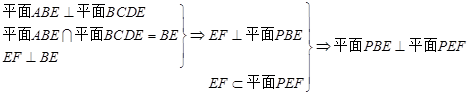
 ,以
,以 为原点,以
为原点,以 方向为
方向为 轴,以
轴,以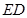 方向为
方向为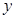 轴,以与平面
轴,以与平面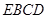 向上的法向量同方向为
向上的法向量同方向为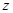 轴,建立空间直角坐标系 7分
轴,建立空间直角坐标系 7分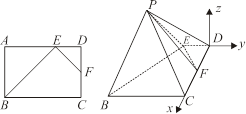
 和平面
和平面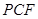 的法向量分别为
的法向量分别为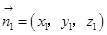 ,
,
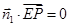 及
及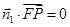 可得到
可得到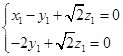 即
即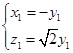 ,不妨取
,不妨取
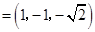
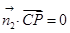 及
及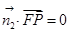 可得到
可得到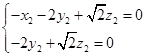 即
即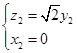
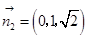 9分
9分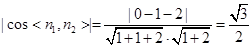 11分
11分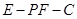 大小为
大小为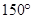 12分.
12分.

 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
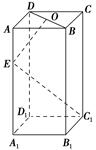
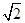 ,OE⊥EC1,求AA1的长.
,OE⊥EC1,求AA1的长.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题

| A.有无数条 | B.有2条 | C.有1条 | D.不存在 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.平面内的一条直线和这平面外的一条直线 |
| B.分别在不同平面内的两条直线 |
| C.不在同一个平面内的两条直线 |
| D.不同在任何一个平面内的两条直线. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com