
【题目】在平面直角坐标系![]() 中,已知向量
中,已知向量![]() ,
,![]() ,且
,且![]() .记动点
.记动点![]() 的轨迹为
的轨迹为![]() .
.
(1)求![]() 的方程;
的方程;
(2)已知直线![]() 过坐标原点,且与(1)中的轨迹
过坐标原点,且与(1)中的轨迹![]() 交于
交于![]() 两点,
两点,![]() 在第三象限,且
在第三象限,且![]() 轴,垂足为
轴,垂足为![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,求
,求![]() 的面积的最大值.
的面积的最大值.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)由![]() 、
、![]() 推出
推出![]() ,可知
,可知![]() 的轨迹是以
的轨迹是以![]() ,
,![]() 为焦点,4为长轴的椭圆,写出椭圆的标准方程即可;(2)设直线
为焦点,4为长轴的椭圆,写出椭圆的标准方程即可;(2)设直线![]() 的方程为
的方程为![]() ,与椭圆方程联立求出M、N、H的坐标及直线HN的方程,直线HN的方程与椭圆方程联立求出Q点坐标从而求出
,与椭圆方程联立求出M、N、H的坐标及直线HN的方程,直线HN的方程与椭圆方程联立求出Q点坐标从而求出![]() 面积的表达式,利用导数研究面积的最大值.
面积的表达式,利用导数研究面积的最大值.
(1)设![]() ,
,![]() ,
,
则![]() ,
,![]() .
.
因为![]() ,所以
,所以![]() ,
,
由椭圆的定义可知![]() 的轨迹是以
的轨迹是以![]() ,
,![]() 为焦点,4为长轴的椭圆.
为焦点,4为长轴的椭圆.
故![]() 的方程为
的方程为![]() .
.
(2)由题意可知直线![]() 的斜率一定存在,设直线
的斜率一定存在,设直线![]() 的方程为
的方程为![]() (
(![]() ),
),
与椭圆![]() 联立可得
联立可得![]() ,
,
所以![]() ,
,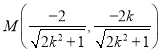 ,
,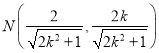 .
.
点![]() 的坐标为
的坐标为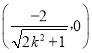 ,直线
,直线![]() 的方程为
的方程为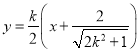 ,
,
代入![]() ,可得
,可得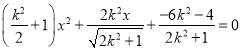 ,
,
所以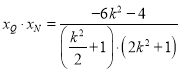 .
.
因为![]() ,所以
,所以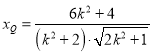 ,
,
![]() 的坐标为
的坐标为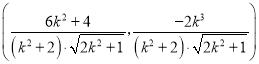 ,
,
于是![]() ,所以
,所以![]() ,即
,即![]() .
.
因为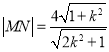 ,
,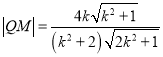 .
.
所以![]() .
.
令![]() ,
, ,
,
由![]() ,可得
,可得![]() ,
,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
因此当![]() 时,函数
时,函数![]() 有最大值,最大值为
有最大值,最大值为![]() ,即
,即![]() 的最大值为
的最大值为![]() .
.


科目:高中数学 来源: 题型:
【题目】“伦敦眼”坐落在英国伦敦泰晤士河畔,是世界上首座观景摩天轮,又称“千禧之轮”,该摩天轮的半径为6(单位:![]() ),游客在乘坐舱
),游客在乘坐舱![]() 升到上半空鸟瞰伦敦建筑
升到上半空鸟瞰伦敦建筑![]() ,伦敦眼与建筑之间的距离
,伦敦眼与建筑之间的距离![]() 为12(单位:
为12(单位:![]() ),游客在乘坐舱
),游客在乘坐舱![]() 看建筑
看建筑![]() 的视角为
的视角为![]() .
.

(1)当乘坐舱![]() 在伦敦眼的最高点
在伦敦眼的最高点![]() 时,视角
时,视角![]() ,求建筑
,求建筑![]() 的高度;
的高度;
(2)当游客在乘坐舱![]() 看建筑
看建筑![]() 的视角
的视角![]() 为
为![]() 时,拍摄效果最好.若在伦敦眼上可以拍摄到效果最好的照片,求建筑
时,拍摄效果最好.若在伦敦眼上可以拍摄到效果最好的照片,求建筑![]() 的最低高度.
的最低高度.
(说明:为了便于计算,数据与实际距离有误差,伦敦眼的实际高度为![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定椭圆C:![]() (
(![]() ),称圆心在原点O,半径为
),称圆心在原点O,半径为![]() 的圆是椭圆C的“卫星圆”.若椭圆C的离心率
的圆是椭圆C的“卫星圆”.若椭圆C的离心率![]() ,点
,点![]() 在C上.
在C上.
(1)求椭圆C的方程和其“卫星圆”方程;
(2)点P是椭圆C的“卫星圆”上的一个动点,过点P作直线![]() ,
,![]() 使得
使得![]()
![]()
![]() ,与椭圆C都只有一个交点,且
,与椭圆C都只有一个交点,且![]() ,
,![]() 分别交其“卫星圆”于点M,N,证明:弦长
分别交其“卫星圆”于点M,N,证明:弦长![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() +
+![]() =1(a>b>0)的两个焦点分别为F1(﹣2,0),F2(2,0),离心率为
=1(a>b>0)的两个焦点分别为F1(﹣2,0),F2(2,0),离心率为![]() .过焦点F2的直线l(斜率不为0)与椭圆C交于A,B两点,线段AB的中点为D,O为坐标原点,直线OD交椭圆于M,N两点.
.过焦点F2的直线l(斜率不为0)与椭圆C交于A,B两点,线段AB的中点为D,O为坐标原点,直线OD交椭圆于M,N两点.
(Ⅰ)求椭圆C的方程;
(Ⅱ)当四边形MF1NF2为矩形时,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (其中
(其中![]() ).
).
(1)当![]() 时,若函数
时,若函数![]() 在
在![]() 上单调递减,求
上单调递减,求![]() 的取值范围;
的取值范围;
(2)当![]() ,
,![]() 时,
时,
①求函数![]() 的极值;
的极值;
②设函数![]() 图象上任意一点处的切线为
图象上任意一点处的切线为![]() ,求
,求![]() 在
在![]() 轴上的截距的取值范围.
轴上的截距的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年是中华人民共和国成立70周年.为了让人民了解建国70周年的风雨历程,某地的民调机构随机选取了该地的100名市民进行调查,将他们的年龄分成6段:![]() ,
,![]() ,…,
,…,![]() ,并绘制了如图所示的频率分布直方图.
,并绘制了如图所示的频率分布直方图.

(1)现从年龄在![]() ,
,![]() ,
,![]() 内的人员中按分层抽样的方法抽取8人,再从这8人中随机选取3人进行座谈,用
内的人员中按分层抽样的方法抽取8人,再从这8人中随机选取3人进行座谈,用![]() 表示年龄在
表示年龄在![]() )内的人数,求
)内的人数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(2)若用样本的频率代替概率,用随机抽样的方法从该地抽取20名市民进行调查,其中有![]() 名市民的年龄在
名市民的年龄在![]() 的概率为
的概率为![]() .当
.当![]() 最大时,求
最大时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某森林公园有一直角梯形区域ABCD,其四条边均为道路,AD∥BC,∠ADC=90°,AB=5千米,BC=8千米,CD=3千米.现甲、乙两管理员同时从![]() 地出发匀速前往D地,甲的路线是AD,速度为6千米/小时,乙的路线是ABCD,速度为v千米/小时.
地出发匀速前往D地,甲的路线是AD,速度为6千米/小时,乙的路线是ABCD,速度为v千米/小时.

(1)若甲、乙两管理员到达D的时间相差不超过15分钟,求乙的速度v的取值范围;
(2)已知对讲机有效通话的最大距离是5千米.若乙先到达D,且乙从A到D的过程中始终能用对讲机与甲保持有效通话,求乙的速度v的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com