
在平面直角坐标系上,设不等式组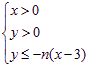 (
(![]() )
)
所表示的平面区域为![]() ,记
,记![]() 内的整点(即横坐标和纵坐标均为整数的点)的个数为
内的整点(即横坐标和纵坐标均为整数的点)的个数为![]() .
.
(Ⅰ)求![]() 并猜想
并猜想![]() 的表达式再用数学归纳法加以证明;
的表达式再用数学归纳法加以证明;
(Ⅱ)设数列![]() 的前
的前![]() 项和为
项和为![]() ,数列
,数列![]() 的前
的前![]() 项和
项和![]() ,是否存在自然数m?使得对一切
,是否存在自然数m?使得对一切![]() ,
,![]() 恒成立。若存在,求出m的值,若不存在,请说明理由。
恒成立。若存在,求出m的值,若不存在,请说明理由。
(Ⅰ)![]() ,
,![]() ,
,![]() ,
,![]() =3n ,(Ⅱ)满足题设的自然数m存在,其值为0
=3n ,(Ⅱ)满足题设的自然数m存在,其值为0
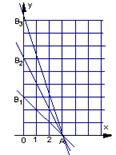
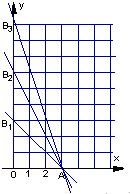
(Ⅰ)当n=1时,D1为Rt△OAB1的内部包括斜边,这时![]()
![]() ,
,
当n=2时,D2为Rt△OAB2的内部包括斜边,这时![]()
![]() ,
,
当n=3时,D3为Rt△OAB3的内部包括斜边,这时![]()
![]() ,……, ---3分
,……, ---3分
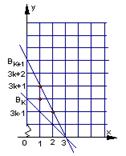 由此可猜想
由此可猜想![]() =3n。 --------------------------------------------------4分
=3n。 --------------------------------------------------4分
下面用数学归纳法证明:
当n=1时,猜想显然成立。
假设当n=k时,猜想成立,即![]() ,(
,(![]() ) ----5分
) ----5分
如图,平面区域![]() 为Rt
为Rt![]() 内部包括斜边、平面区域
内部包括斜边、平面区域![]() 为
为
Rt△![]() 内部包括斜边,∵平面区域
内部包括斜边,∵平面区域![]() 比平面区域
比平面区域![]() 多3
多3
个整点, ------- 7分
即当n=k+1时,![]() ,这就是说当n=k+1时,
,这就是说当n=k+1时,
猜想也成立,
由(1)、(2)知![]() =3n对一切
=3n对一切![]() 都成立。 ---------------------8分
都成立。 ---------------------8分
(Ⅱ)∵![]() =3n, ∴数列
=3n, ∴数列![]() 是首项为3,公差为3的等差数列,
是首项为3,公差为3的等差数列,
∴![]() .
.
![]() -------------------------10分
-------------------------10分
![]()
![]()
=![]() =
=![]() -------------------------------11分
-------------------------------11分
∵对一切![]() ,
,![]() 恒成立, ∴
恒成立, ∴![]()
∵![]() 在
在![]() 上为增函数 ∴
上为增函数 ∴![]() ---13分
---13分
![]() ,满足
,满足![]() 的自然数为0,
的自然数为0,
∴满足题设的自然数m存在,其值为0。 -------------------------14分


 全能练考卷系列答案
全能练考卷系列答案科目:高中数学 来源: 题型:
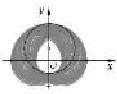 如图,阴影是集合P={(x,y)|(x-cosθ)2+(y-sinθ)2=4,0≤θ≤π}在平面直角坐标系上表示的点集,则阴影中间形如“水滴”部分的面积等于( )
如图,阴影是集合P={(x,y)|(x-cosθ)2+(y-sinθ)2=4,0≤θ≤π}在平面直角坐标系上表示的点集,则阴影中间形如“水滴”部分的面积等于( )A、π+
| ||||
B、
| ||||
C、
| ||||
| D、π+2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 在平面直角坐标系上,设不等式组
在平面直角坐标系上,设不等式组
|
| 1 |
| Sn |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
|
| 1 |
| anan+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com