
分析 设Pn+1(n+1,an+1),则PnPn+1=(1,an+1-an)=(1,2),即an+1-an=2,由等差数列的通项公式和求和公式即可得到所求和.
解答 解:设Pn+1(n+1,an+1),
则PnPn+1=(1,an+1-an)=(1,2),
即an+1-an=2,
所以数列{an}是以2为公差的等差数列.
又因为a1+2a2=3,即3a1+2×2=3,
所以a1=-$\frac{1}{3}$,
所以Sn=-$\frac{1}{3}$n+$\frac{1}{2}$n(n-1)•2
=n(n-$\frac{4}{3}$).
故答案为:n(n-$\frac{4}{3}$).
点评 本题考查等差数列的通项公式和求和公式的运用,考查新定义的理解和运用,考查运算能力,属于中档题.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 增函数,奇函数 | B. | 减函数,奇函数 | ||
| C. | 非奇非偶的增函数 | D. | 非奇非偶的减函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
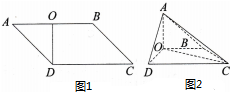 如图1,在∠A=45°的平行四边形ABCD中,DO垂直平分AB,且AB=2,现将△ADO沿DO折起(如图2),使AC=$\sqrt{6}$.
如图1,在∠A=45°的平行四边形ABCD中,DO垂直平分AB,且AB=2,现将△ADO沿DO折起(如图2),使AC=$\sqrt{6}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com