
分析 (1)利用向量数量积的运算法则化简已知可得:($\sqrt{2}a$-c)cosB=bcosC,然后利用正弦定理化简后,根据sinA不为0得到cosB的值,根据B的范围及特殊角的三角函数值即可求出B的度数;
(2)根据向量的减法法则由|$\overrightarrow{BA}-\overrightarrow{BC}$|=$\sqrt{3}$,得到|$\overrightarrow{CA}$|=$\sqrt{3}$,即得到b的平方等于3,然后根据余弦定理表示出b的平方,把b的平方代入后,利用基本不等式即可求出ac的最大值,根据三角形的面积公式,利用ac的最大值及B的度数求出sinB的值,即可得到面积的最大值.
解答 解:(1)(c-$\sqrt{2}a$)$\overrightarrow{BA}•\overrightarrow{BC}$=c$\overrightarrow{AC}•\overrightarrow{CB}$可化为:($\sqrt{2}a$-c)cosB=bcosC,
根据正弦定理有:($\sqrt{2}$sinA-sinC)cosB=sinBcosC,
即$\sqrt{2}$sinAcosB=sinA,
因为sinA>0,所以cosB=$\frac{\sqrt{2}}{2}$,即B=$\frac{π}{4}$;
(2)因为|$\overrightarrow{BA}-\overrightarrow{BC}$|=$\sqrt{3}$,所以|$\overrightarrow{CA}$|=$\sqrt{3}$,即b2=3,
根据余弦定理b2=a2+c2-2accosB,
可得a2+c2-$\sqrt{2}$ac=3,
由基本不等式可知3=a2+c2-$\sqrt{2}$ac≥(2-$\sqrt{2}$)ac,
即ac≤$\frac{3}{2}$(2-$\sqrt{2}$),
故△ABC的面积S=$\frac{1}{2}acsinB$=$\frac{\sqrt{2}}{4}$ac≤$\frac{3\sqrt{2}+3}{4}$,
即当a=c时,△ABC的面积的最大值为$\frac{3\sqrt{2}+3}{4}$.
点评 此题考查学生灵活运用平面向量的数量积的运算法则,灵活运用正弦、余弦定理及三角形的面积公式化简求值,是一道综合题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
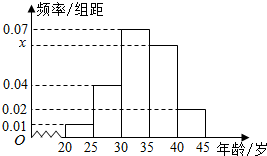 为增强市民的节能环保意识,某市面向全市征召义务宣传志愿者,从符合条件的1000名志愿者中随机抽取100名志愿者,其中年龄频率分布直方图如图所示,其中x=3y,且年龄分组区间为:[[20,25],[25,30),[30,35),[35,40),[40,45].
为增强市民的节能环保意识,某市面向全市征召义务宣传志愿者,从符合条件的1000名志愿者中随机抽取100名志愿者,其中年龄频率分布直方图如图所示,其中x=3y,且年龄分组区间为:[[20,25],[25,30),[30,35),[35,40),[40,45].查看答案和解析>>
科目:高中数学 来源: 题型:选择题
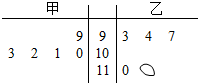 甲、乙两同学用茎叶图记录高三前5次数学测试的成绩,如图所示.他们在分析对比成绩变化时,发现乙同学成绩的一个数字看不清楚了,若已知乙的平均成绩低于甲的平均成绩,则看不清楚的数字为( )
甲、乙两同学用茎叶图记录高三前5次数学测试的成绩,如图所示.他们在分析对比成绩变化时,发现乙同学成绩的一个数字看不清楚了,若已知乙的平均成绩低于甲的平均成绩,则看不清楚的数字为( )| A. | 0 | B. | 3 | C. | 6 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | $\sqrt{3}-1$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1-2i | B. | 1+2i | C. | -1-2i | D. | -1+2i |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com