练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知函数，设f（x）的最大值、最小值分别为m，n，若m-n＜1，则正整数a的取值个数是（ ）
    A．1
    B．2
    C．3
    D．4
    【答案】分析：先将函数平方，然后利用基本不等式和二次函数的单调性求出函数的最值，最后根据m-n＜1建立不等式关系，求出所求．
    解答：解：∵≥0
    ∴[f（x）]2=2a+2≥2a，
    当x=0 或2a时f（x）取最小值n=
    又2≤2a-x+x=2a，当x=2a-x即x=a时取等号
    即f（x）2≤2a+2a=4a，f（x）≤2，当x=a时取最大值m=2
    这样m-n=2-＜1
    ＜=
    因此只能取a=1 或 2
    共2个正整数．
    故选B．
    点评：本题主要考查了函数的最值及其几何意义，以及不等式的应用，同时考查了分析问题的能力，属于中档题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2010年高三数学调研试卷（理科）（解析版） 题型：解答题

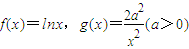    已知函数，设F（x）=f（x）+g（x）．
    （1）求F（x）的单调区间；
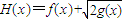    （2）若以，图象上任意一点P（x，y）为切点的切线的斜率k≤1恒成立，求实数a的最小值；
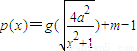    （3）是否存在实数m，使得函数的图象与q（x）=f（1+x2）的图象恰好有四个不同的交点？若存在，求出m的取值范围，若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年江苏省连云港市东海县高级中学高三（上）期末数学模拟试卷（一）（解析版） 题型：解答题

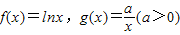    已知函数，设F（x）=f（x）+g（x）
    （1）求F（x）的单调区间；
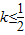    （2）若以y=F（x）（x∈（0，3]）图象上任意一点P（x，y）为切点的切线的斜率恒成立，求实数a的最小值；
    （3）若对所有的x∈[e，+∞）都有xf（x）≥ax-a成立，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源：2013年上海市徐汇、松江、金山区高考数学二模试卷（文科）（解析版） 题型：选择题

    已知函数，设F（x）=x2•f（x），则F（x）是（ ）
    A．奇函数，在（-∞，+∞）上单调递减
    B．奇函数，在（-∞，+∞）上单调递增
    C．偶函数，在（-∞，0）上递减，在（0，+∞）上递增
    D．偶函数，在（-∞，0）上递增，在（0，+∞）上递减

    查看答案和解析>>

    科目：高中数学 来源：2011年江苏省苏北四市高三第二次联考数学模拟试卷（一）（解析版） 题型：解答题

    已知函数，设F（x）=f（x）+g（x）
    （1）求F（x）的单调区间；
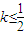    （2）若以y=F（x）（x∈（0，3]）图象上任意一点P（x，y）为切点的切线的斜率恒成立，求实数a的最小值；
    （3）若对所有的x∈[e，+∞）都有xf（x）≥ax-a成立，求实数a的取值范围．

    查看答案和解析>>

    同步练习册答案