练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    不等式2x2-x-1＜0成立的一个必要不充分条件是


    1. A.
      数学公式
    2. B.
      数学公式
    3. C.
      （1，+∞）
    4. D.
      （-1，1）
    D
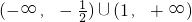
    分析：根据一元二次不等式的解法，可得2x2-x-1＜0的解集为{x|-＜x＜1}，进而依次分析选项，判断选项所给的不等式与-＜x＜1的关系，可判断选项．
    解答：对于不等式2x2-x-1＜0，解可得-＜x＜1，即3x2-2x-1＜0的解集为{x|-＜x＜1}，
    根据题意，分析选项可得，
    A中，当-＜x＜1时，必有2x2-x-1＜0成立，若有2x2-x-1＜0成立，则-＜x＜1一定成立，即-＜x＜1是“3x2-2x-1＜0”成立的充分必要条件；
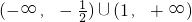    B中，当x∈时，2x2-x-1＜0不成立，反之若有2x2-x-1＜0成立，则必有x＞1或x＜- 不成立，即x＞1或x＜-是“2x2-x-1＜0”成立的既不充分也不必要条件；
    C中，当1＜x时，2x2-x-1＜0一定成立，反之若有2x2-x-1＜0成立，则1＜x不一定成立，1＜x是2x2-x-1＜0成立充分不必要条件；
    D中，当-1＜x＜1时，2x2-x-1＜0不一定成立，反之若有2x2-x-1＜0成立，则-1＜x＜0一定成立，即-1＜x＜0是3x2-2x-1＜0成立的必要不充分条件；
    故选D．
    点评：本题考查充分、必要条件的判断，涉及一元二次不等式的解法；解题的关键要掌握充分、必要条件定义．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    不等式2x2-x-1＞0的解集是（　　）
    A、(-
    1
    2
    ，1)
    B、（1，+∞）
    C、（-∞，1）∪（2，+∞）
    D、(-∞，-
    1
    2
    )    ∪（1，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    不等式2x2-x-1＜0成立的一个必要不充分条件是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    不等式
    2x2-x-1
    (x-1)|x|
    ≥0的解集为
    {x|x＞1或0＜x＜1或-
    1
    2
    ≤x＜0    }
    {x|x＞1或0＜x＜1或-
    1
    2
    ≤x＜0    }
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    不等式2x2-x-1＞0的解集是
    (-∞，-
    1
    2
    )∪(1，+∞)
    (-∞，-
    1
    2
    )∪(1，+∞)
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    不等式2x2-x≤1的解集为（　　）

    查看答案和解析>>

    同步练习册答案