
分析 按照给出的定义对四个命题结合数列的知识逐一进行判断真假,①列举即可;②需举反例;③可用数学归纳法加以证明;④可由归纳推理判断其正误.
解答 解:①当a=5时,x1=5,x2=$[\frac{5+[\frac{5}{5}]}{2}]$=3,x3=$[\frac{3+[\frac{5}{3}]}{2}]$=2,故正确;
②令a=3,则x1=3,
∴x2=$[\frac{3+[\frac{3}{3}]}{2}]$=2,x3=$[\frac{2+[\frac{3}{2}]}{2}]$=1,x4=$[\frac{1+[\frac{3}{1}]}{2}]$=2,…,
即以后各项均为1、2交替出现,故不正确;
③当n=1时,x1=a,
∵a-($\sqrt{a}$-1)=$(\sqrt{a}-\frac{1}{2})^{2}$+$\frac{3}{4}$>0,
∴x1=a>$\sqrt{a}$-1成立;
假设当n=k(k≥2)时,xk>$\sqrt{a}$-1,
∵$\frac{{x}_{k}+[\frac{a}{{x}_{k}}]}{2}$>$\frac{\sqrt{a}-1+[\frac{a}{\sqrt{a}-1}]}{2}$>$\sqrt{a}$-1,
∴xk+1=$[\frac{{x}_{k}+[\frac{a}{{x}_{k}}]}{2}]$≥$[\sqrt{a}-\frac{1}{2}]$>$\sqrt{a}$-1,
即当n=k+1时,结论亦成立;
综上所述,对任意正整数n,当n≥1时,xn>$\sqrt{a}$-1,故正确;
④∵xk+1=$[\frac{{x}_{k}+[\frac{a}{{x}_{k}}]}{2}]$≥xk,
∴由①、②规律可知结论成立.
故答案为:①③④.
点评 本题主要考查了数列递推公式的应用,归纳推理和演绎推理的方法,直接证明和间接证明方法,数学归纳法的应用,难度较大,需有较强的推理和思维能力,注意解题方法的积累,属于难题.


 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知函数f(x)为定义域为R的偶函数,当x≥0时,f(x)=2-x+2-4
已知函数f(x)为定义域为R的偶函数,当x≥0时,f(x)=2-x+2-4查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
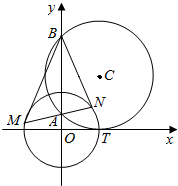 如图,圆C与x轴相切于点T(1,0),与y轴正半轴交于两点A,B(B在A的上方),且|AB|=2.过点A任作一条直线与圆O:x2+y2=1相交于M,N两点,则$\frac{|NB|}{|NA|}$-$\frac{|MA|}{|MB|}$=2.
如图,圆C与x轴相切于点T(1,0),与y轴正半轴交于两点A,B(B在A的上方),且|AB|=2.过点A任作一条直线与圆O:x2+y2=1相交于M,N两点,则$\frac{|NB|}{|NA|}$-$\frac{|MA|}{|MB|}$=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com