
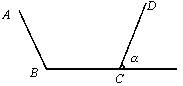
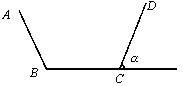
某村欲建一横截面为等腰梯形的水渠(渠长一定),为降低成本,必须适当减少水渠的侧壁与底面面积之和。若水渠的断面面积设计为定值am2,渠深为1m,问水渠的侧壁的侧角a应为多少时,才能使修建成本最低?
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源: 题型:
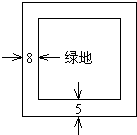 (2003•海淀区一模)某小区欲建一面积为640平方米的矩形绿地,四周有小路,绿地长边外小路宽5米,短边外小路宽8米(如图),求怎样设计绿地的长宽使绿地和小路总占地面积最小?
(2003•海淀区一模)某小区欲建一面积为640平方米的矩形绿地,四周有小路,绿地长边外小路宽5米,短边外小路宽8米(如图),求怎样设计绿地的长宽使绿地和小路总占地面积最小?查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:044

查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:044
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
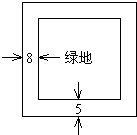 某小区欲建一面积为640平方米的矩形绿地,四周有小路,绿地长边外小路宽5米,短边外小路宽8米(如图),求怎样设计绿地的长宽使绿地和小路总占地面积最小?
某小区欲建一面积为640平方米的矩形绿地,四周有小路,绿地长边外小路宽5米,短边外小路宽8米(如图),求怎样设计绿地的长宽使绿地和小路总占地面积最小?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com