
A.α>β B.α=β C.α<β D.不能确定
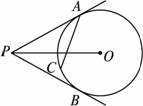
图2-4-15
科目:高中数学 来源: 题型:
| 序号 | 分组(分数段) | 频数(人数) | 频率 |
| 1 | [0,60) | a | 0.1 |
| 2 | [60,75) | 15 | b |
| 3 | [75,90) | 20 | 0.4 |
| 4 | [90,100] | c | d |
| 合计 | 50 | 1 | |
查看答案和解析>>
科目:高中数学 来源: 题型:
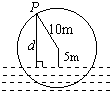 如图,一个半径为10米的水轮按逆时针方向每分钟转4圈.记水轮上的点P到水面的距离为d米(P在水面下则d为负数),则d(米)与时间t(秒)之间满足关系式:d=Asin(ωt+φ)+k(A>0,ω>0),-
如图,一个半径为10米的水轮按逆时针方向每分钟转4圈.记水轮上的点P到水面的距离为d米(P在水面下则d为负数),则d(米)与时间t(秒)之间满足关系式:d=Asin(ωt+φ)+k(A>0,ω>0),-| π |
| 2 |
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图:过抛物线y2=4x上的点A(1,2)作切线l交x轴与直线x=-4分别于D,B.动点P是抛物线y2=4x上的一点,点E在线段AP上,满足
如图:过抛物线y2=4x上的点A(1,2)作切线l交x轴与直线x=-4分别于D,B.动点P是抛物线y2=4x上的一点,点E在线段AP上,满足| AE |
| EP |
| BF |
| FP |
查看答案和解析>>
科目:高中数学 来源: 题型:
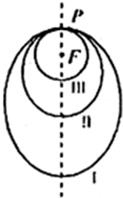 给出下列5个命题:
给出下列5个命题:| 1 |
| 5 |
| 1 |
| 1-a |
| 2a |
tan2x+
| ||
|
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:

图2-15
A.2 B
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com