
分析 由题意可知y′≥0在(0,+∞)上恒成立,分离参数得a≥$\frac{1}{x}-\frac{1}{2{x}^{2}}=\frac{2x-1}{2{x}^{2}}$,求出右侧函数的最大值即可得出a的范围.
解答 解:y′=$\frac{1}{x}+2ax-2$,x∈(0,+∞),
∵曲线y=lnx+ax2-2x(a为常数)不存在斜率为负数的切线,
∴y′=$\frac{1}{x}+2ax-2$≥0在(0,+∞)上恒成立,
∴a≥$\frac{1}{x}-\frac{1}{2{x}^{2}}=\frac{2x-1}{2{x}^{2}}$恒成立,x∈(0,+∞).
令f(x)=$\frac{2x-1}{2{x}^{2}}$,x∈(0,+∞),则f′(x)=$\frac{1-x}{{x}^{3}}$,
∴当0<x<1时,f′(x)>0,当x>1时,f′(x)<0,
∴f(x)在(0,1)上单调递增,在(1,+∞)上单调递减,
∴当x=1时,f(x)=$\frac{2x-1}{2{x}^{2}}$取得最大值f(1)=$\frac{1}{2}$,
∴a$≥\frac{1}{2}$.
故答案为[$\frac{1}{2}$,+∞).
点评 本题考查了导数的几何意义,导数与函数单调性的关系,函数最值的计算,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
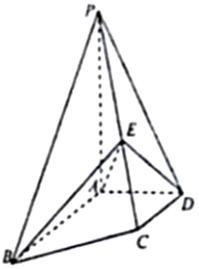 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB∥DC,DA⊥AB,AB=AP=2,DA=DC=1,E为PC上一点,且PE=$\frac{2}{3}$PC.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB∥DC,DA⊥AB,AB=AP=2,DA=DC=1,E为PC上一点,且PE=$\frac{2}{3}$PC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
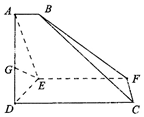 如图,已知梯形CDEF与△ADE所在平面垂直,AD⊥DE,CD⊥DE,AB∥CD∥EF,AE=2DE=8,AB=3,EF=9.CD=12,连接BC,BF.
如图,已知梯形CDEF与△ADE所在平面垂直,AD⊥DE,CD⊥DE,AB∥CD∥EF,AE=2DE=8,AB=3,EF=9.CD=12,连接BC,BF.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
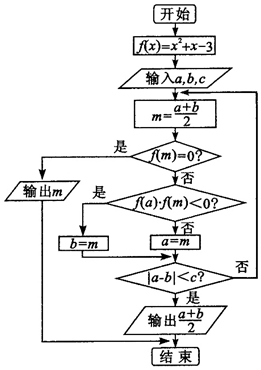
| A. | 1.125 | B. | 1.25 | C. | 1.3125 | D. | 1.375 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 169石 | B. | 192石 | C. | 1367石 | D. | 1164石 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2n | B. | 1 | C. | $\frac{1}{2}$ | D. | $\frac{n}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -4-3i | B. | 4-3i | C. | 4+3i | D. | -4+3i |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com