
在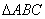 中,
中,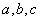 分别为角
分别为角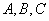 的对边,设
的对边,设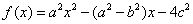 ,
,
(1)若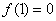 ,且
,且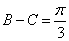 ,求角
,求角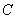 的大小;(2)若
的大小;(2)若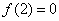 ,求角
,求角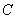 的取值范围。
的取值范围。
解:(1)由 f(1)=0,得a2-a2+b2-4c2=0,∴b=2c
又由正弦定理,得b=2RsinB,c=2RsinC,将其代入上式,得sinB=2sinC
∵B-C=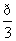 ∴B=
∴B=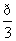 +C,将其代入上式,得sin(
+C,将其代入上式,得sin(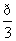 +C)=2sinC
+C)=2sinC
∴sin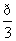 cosC+cos
cosC+cos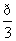 sinC=2sinC,整理得,
sinC=2sinC,整理得,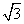 sinC=cosC,∴tanC=
sinC=cosC,∴tanC=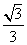
∵角C是三角形的内角,∴C=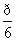 ---------------6分
---------------6分
(2)∵ f(2)=0,∴4a2-2a2+2b2-4c2=0,即a2+b2-2c2=0 ------7分
由余弦定理,得cosC=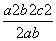 =
=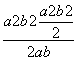
∴cosC=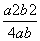 ≥
≥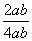 =
=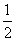 (当且仅当a=b时取等号) ---------------------10分
(当且仅当a=b时取等号) ---------------------10分
∴cosC≥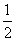 ,∠C是锐角,又∵余弦函数在(0,
,∠C是锐角,又∵余弦函数在(0,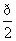 )上递减,∴0<C≤
)上递减,∴0<C≤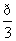 ---------12分
---------12分


科目:高中数学 来源: 题型:
已知函数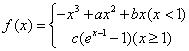 在
在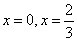 处存在极值。
处存在极值。
(1)求实数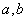 的值;
的值;
(2)函数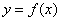 的图像上存在两点A,B使得
的图像上存在两点A,B使得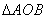 是以坐标原点O为直角顶点的直角三角形,且斜边AB的中点在
是以坐标原点O为直角顶点的直角三角形,且斜边AB的中点在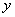 轴上,求实数
轴上,求实数 的取值范围;
的取值范围;
(3)当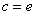 时,讨论关于
时,讨论关于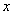 的方程
的方程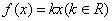 的实根个数。
的实根个数。
查看答案和解析>>
科目:高中数学 来源: 题型:
某种计算机病毒是通过电子邮件进行传播的,下表是某公司前5天监测到的数据:
| 第 | 1 | 2 | 3 | 4 | 5 |
| 被感染的计算机数量 | 10 | 20 | 39 | 81 | 160 |
则下列函数模型中能较好地反映计算机在第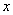 天被感染的数量
天被感染的数量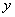 与
与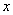 之间的关系的是( )
之间的关系的是( )
A.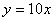 B.
B.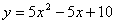
C.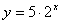 D.
D.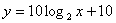
查看答案和解析>>
科目:高中数学 来源: 题型:
某工厂在试验阶段大量生产一种零件,这种零件有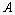 、
、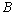 两项技术指标需要检测,设各项技术指标达标与否互不影响.若有且仅有一项技术指标达标的概率为
两项技术指标需要检测,设各项技术指标达标与否互不影响.若有且仅有一项技术指标达标的概率为 ,至少一项技术指标达标的概率为
,至少一项技术指标达标的概率为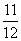 .按质量检验规定:两项技术指标都达标的零件为合格品.
.按质量检验规定:两项技术指标都达标的零件为合格品.
(Ⅰ)求一个零件经过检测为合格品的概率是多少?
(Ⅱ)任意依次抽取该种零件4个,设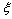 表示其中合格品的个数,求
表示其中合格品的个数,求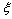 的分布列及数学期望
的分布列及数学期望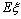 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com