
已知函数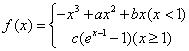 在
在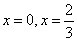 处存在极值。
处存在极值。
(1)求实数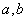 的值;
的值;
(2)函数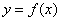 的图像上存在两点A,B使得
的图像上存在两点A,B使得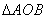 是以坐标原点O为直角顶点的直角三角形,且斜边AB的中点在
是以坐标原点O为直角顶点的直角三角形,且斜边AB的中点在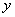 轴上,求实数
轴上,求实数 的取值范围;
的取值范围;
(3)当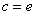 时,讨论关于
时,讨论关于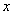 的方程
的方程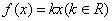 的实根个数。
的实根个数。
解:(1)当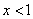 时,
时,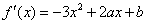 .………………1分
.………………1分
因为函数 在
在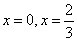 处存在极值,所以
处存在极值,所以
解得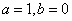 .………………4分
.………………4分
(2) 由(I)得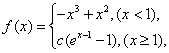
根据条件知A,B的横坐标互为相反数,不妨设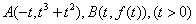 .
.
若 ,则
,则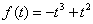 ,
,
由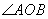 是直角得,
是直角得,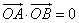 ,即
,即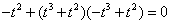 ,
,
即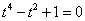 .此时无解;………………6分
.此时无解;………………6分
若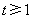 ,则
,则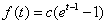 . 由于AB的中点在
. 由于AB的中点在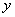 轴上,且
轴上,且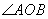 是直角,所以B点不可能在
是直角,所以B点不可能在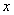 轴上,即
轴上,即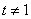 . 同理有
. 同理有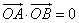 ,即
,即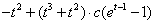 =0,
=0, 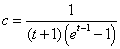 .
.
因为函数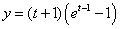 在
在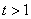 上的值域是
上的值域是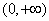 ,
,
所以实数 的取值范围是
的取值范围是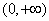 .………………8分
.………………8分
(3)由方程 ,知
,知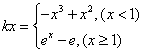 ,可知0一定是方程的根,…10分
,可知0一定是方程的根,…10分
所以仅就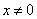 时进行研究:方程等价于
时进行研究:方程等价于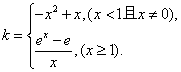
构造函数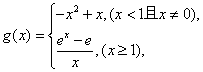
对于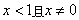 部分,函数
部分,函数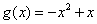 的图像是开口向下的抛物线的一部分,
的图像是开口向下的抛物线的一部分,
当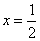 时取得最大值
时取得最大值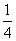 ,其值域是
,其值域是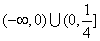 ;
;
对于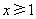 部分,函数
部分,函数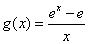 ,由
,由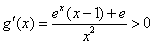 ,
,
知函数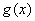 在
在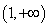 上单调递增.
上单调递增.
所以,①当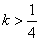 或
或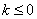 时,方程
时,方程 有两个实根;
有两个实根;
②当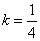 时,方程
时,方程 有三个实根;
有三个实根;
③当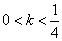 时,方程
时,方程 有四个实根. ……
有四个实根. ……


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com