
分析 (1)利用等差数列的通项公式及其求和公式即可得出.
(2)利用等差数列的求和公式、二次函数的单调性即可得出.
解答 解:(1)设等差数列{an}的公差为d,
则由a1=-15,${s_5}=5{a_1}+\frac{5×4}{2}d$,
得-15×5+10d=-55,
解得d=2,
∴an=-15+(n-1)•2=2n-17,
∴数列{an}的通项公式为an=2n-17.
(2)由(1)得${S_n}=\frac{n(-15+2n-17)}{2}={n^2}-16n$,
∵${S_n}={n^2}-16n={(n-8)^2}-64≥-64$,
∴对于任意的n∈N*,Sn≥-64恒成立,
∴若不等式Sn>t对于任意的n∈N*恒成立,则只需t<-64,
因此所求实数t的取值范围为(-∞,-64).
点评 本题考查了等差数列的通项公式及其求和公式、二次函数的单调性,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
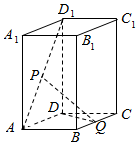 如图,已知直四棱柱ABCD-A1B1C1D1的底面ABCD为菱形,且∠BCD=60°,P为AD1的中点,Q为BC的中点
如图,已知直四棱柱ABCD-A1B1C1D1的底面ABCD为菱形,且∠BCD=60°,P为AD1的中点,Q为BC的中点查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{25}$ | B. | -$\frac{7}{25}$ | C. | 1 | D. | $\frac{\sqrt{7}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,1] | B. | [0,2] | C. | (-2,2] | D. | [0,$\frac{1}{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 0 | 1 | 2 | 3 |
| y | 1 | 3 | 5 | 7 |
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com