
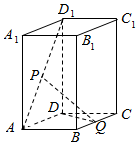
 如图,已知直四棱柱ABCD-A1B1C1D1的底面ABCD为菱形,且∠BCD=60°,P为AD1的中点,Q为BC的中点
如图,已知直四棱柱ABCD-A1B1C1D1的底面ABCD为菱形,且∠BCD=60°,P为AD1的中点,Q为BC的中点分析 (1)过P作PM∥AD交D1D于M,连接MC,则M为D1D的中点,证明四边形PMCQ是平行四边形,可得PQ∥MC,即可证明PQ∥平面D1DCC1;
(2)证明B1B⊥DQ,DQ⊥BC,利用线面垂直的判定定理证明:DQ⊥平面B1BCC1.
解答  证明:(1)过P作PM∥AD交D1D于M,连接MC,则M为D1D的中点,
证明:(1)过P作PM∥AD交D1D于M,连接MC,则M为D1D的中点,
∴PM∥AD,PM=$\frac{1}{2}$AD,
∵AD∥BC,Q为BC的中点,
∴PM∥QC,PM=QC,
∴四边形PMCQ是平行四边形,
∴PQ∥MC,
∵PQ?平面DCC1D1,MC?平面DCC1D1,
∴PQ∥平面DCC1D1.
(2)在直四棱柱ABCD-A1B1C1D1中,B1B⊥平面ABCD,DQ?平面ABCD,
∴B1B⊥DQ,
在菱形ABCD中,DC=BC,∠BCD=60°,∴△BCD为正三角形,故DB=DC,
∵Q为BC的中点,
∴DQ⊥BC,
∵B1B∩BC=B,
∴DQ⊥平面B1BCC1.
点评 本题考查线面平行、垂直的判定定理,考查学生分析解决问题的能力,正确运用线面平行、垂直的判定定理是关键.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源: 题型:解答题
 如图,直四棱柱ABCD-A1B1C1D1中,底面为直角梯形,∠BAD=90°,且AB=BC=AA1=10,AD=2DC=8.
如图,直四棱柱ABCD-A1B1C1D1中,底面为直角梯形,∠BAD=90°,且AB=BC=AA1=10,AD=2DC=8.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$,$\frac{1}{6}$ | B. | $\frac{1}{4}$,$\frac{1}{5}$ | C. | $\frac{1}{3}$,$\frac{1}{4}$ | D. | $\frac{1}{2}$,$\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 510 | B. | -511 | C. | 512 | D. | -512 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=x3,x∈R | B. | y=sinx,x∈R | C. | y=-x,x∈R | D. | y=($\frac{1}{2}$)x,x∈R |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$x-y=0 | B. | 2x-y=0 | C. | x+2y-10=0 | D. | x-2y-8=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 如果m?α,n?α,m、n是异面直线,那么n∥α | |
| B. | 如果m?α,n?α,m、n是异面直线,那么n与α相交 | |
| C. | 如果m?α,n∥α,m、n共面,那么m∥n | |
| D. | 如果m?α,n∥m,那么n∥α |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com