练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知函数，.

    （Ⅰ）求的最小正周期；

    （Ⅱ）求在闭区间上的最大值和最小值.

     

    （Ⅰ）；（Ⅱ）在闭区间上的最大值为，最小值为.

    【解析】

    试题分析：（Ⅰ）将降次化一，化为的形式，然后利用求周期的公式即可得周期；（Ⅱ）由（Ⅰ）可得，又的范围为，由此可得的范围，进而结合图象可求得求在闭区间上的最大值和最小值.

    试题解析：【解析】
    （Ⅰ）由已知，有

    所以，的最小正周期

    （Ⅱ）因为在区间上是减函数，在区间上是增函数. ...8分

    根据图像的对称性知其最小与最大值分别为：，.

    所以，函数在闭区间上的最大值为，最小值为

    考点：1、三角恒等变换；2、三角函数的周期及最值.

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2015届四川省资阳市高二下学期期末考试理科数学试卷（解析版） 题型：选择题

    已知命题p：，.则为

    A．， B．，

    C．， D．，

     

    查看答案和解析>>

    科目：高中数学 来源：2015届四川省高二下学期期中考试理科数学试卷（解析版） 题型：选择题

    函数,则（ ）．

    A． B． C． D．

     

    查看答案和解析>>

    科目：高中数学 来源：2015届四川省高二下学期期中考试文科数学试卷（解析版） 题型：选择题

    在上可导的函数的图形如图所示，则关于的不等式的解集为（ ）．

    A、 B、

    C、 D、

     

    查看答案和解析>>

    科目：高中数学 来源：2015届四川省成都市高新区高三9月月考理科数学试卷（解析版） 题型：解答题

    已知函数（为常数）的图象与轴交于点，曲线在点处的切线斜率为.

    （Ⅰ）求的值及函数的极值；

    （Ⅱ）证明：当时，；

    （Ⅲ）证明：对任意给定的正数，总存在，使得当，恒有.

     

    查看答案和解析>>

    科目：高中数学 来源：2015届四川省成都市高新区高三9月月考理科数学试卷（解析版） 题型：填空题

    某中学为了解高三学生对参加某项社会实践活动的意向，拟采用分层抽样的方法，从高三的四个班的学生中抽取一个容量为100的样本进行调查.已知一、二、三、四班的学生人数之比为4：5：5：6，则应从一班学生中抽取____ ___名学生.

     

    查看答案和解析>>

    科目：高中数学 来源：2015届四川省成都市高新区高三9月月考理科数学试卷（解析版） 题型：选择题

    设是公比为的等比数列，则“为递增数列”是“”的（ ）

    （A）充分而不必要条件 （B）必要而不充分条件

    （C）充分必要条件 （D）既不充分也不必要条件

     

    查看答案和解析>>

    科目：高中数学 来源：2015届四川省成都市高新区高三9月月考文科数学试卷（解析版） 题型：选择题

    已知，若是的最小值，则的取值范围为（ ）

    （A）[-1,2] （B）[-1，0] （C）[1，2] （D）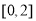

     

    查看答案和解析>>

    科目：高中数学 来源：2015届四川省成都市毕业班摸底测试文科数学试卷（解析版） 题型：选择题

    已知函数(ω＞0)的图象与直线y＝－2的两个相邻公共点之间的距离等于π，则的单调递减区间是( )

    A、 B、

    C、 D、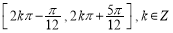

     

    查看答案和解析>>

    同步练习册答案