解:(1)令x=y=0,由f(x+y)=f(x)+f(y),得f(0)=f(0)+f(0),
所以f(0)=0,
令y=-x,则f(0)=f(x)+f(-x),即f(x)+f(-x)=0,
所以f(-x)=-f(x),
故f(x)为奇函数;
(2)任取x
1,x
2,且x
1<x
2,
则f(x
2-x
1)=f[x
2+(-x
1)]=f(x
2)+f(-x
1)=f(x
2)-f(x
1),
由x>0时,f(x)<0,且x
2-x
1>0,
所以f(x
2-x
1)<0,即f(x
2)-f(x
1)<0,
所以f(x
2)<f(x
1),
故f(x)为减函数;
(3)不等式
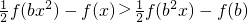
可变为

f(bx
2)-

f(b
2x)>f(x)-f(b)=f(x-b),
?f(bx
2-b
2x)>f(2x-2b),
由(2)知f(x)单调递减,
所以bx
2-b
2x<2x-2b,即bx
2-(b
2+2)x+2b<0,
当b=0时,原不等式解集(0,+∞);
当
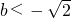
时,原不等式解集
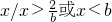
;
当
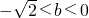
时,原不等式解集

;
当
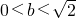
时,原不等式解集
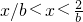
;
当

时,原不等式解集
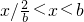
;
分析:(1)利用定义:令x=y=0,可求得f(0),令y=-x,可得f(x)与f(-x)的关系,由奇偶性的定义即可作出判断;
(2)任取x
1,x
2,且x
1<x
2,由x>0时,f(x)<0可判断f(x
2-x
1)的符号,从而可得f(x
2)与f(x
1)的大小关系,由单调性定义即可作出判断;
(3)利用函数的奇偶性、单调性可把不等式转化为具体二次不等式,由b
2≠2分类讨论即可解得;
点评:本题考查抽象函数的奇偶性、单调性的判断,考查抽象不等式的求解,考查分类讨论思想,考查学生解决问题的能力.

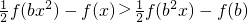 ,(b2≠2).
,(b2≠2).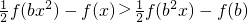 可变为
可变为 f(bx2)-
f(bx2)- f(b2x)>f(x)-f(b)=f(x-b),
f(b2x)>f(x)-f(b)=f(x-b),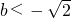 时,原不等式解集
时,原不等式解集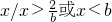 ;
;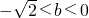 时,原不等式解集
时,原不等式解集 ;
;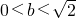 时,原不等式解集
时,原不等式解集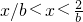 ;
; 时,原不等式解集
时,原不等式解集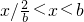 ;
;
