Question

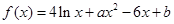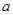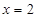已知函数（，为常数），且为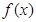的一个极值点．

(Ⅰ) 求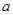的值；

(Ⅱ) 求函数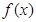的单调区间；

(Ⅲ) 若函数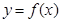有3个不同的零点，求实数的取值范围．

 

Answer 1

【答案】

解： (Ⅰ) 函数f (x)的定义域为（0，+∞）……1分

 ∵ f ′ (x) =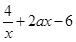              ……….2分

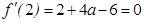∴，则a = 1．……….4分 

(Ⅱ)由(Ⅰ) 知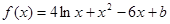

∴ f ′ (x) =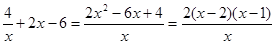   ………6分 

由f ′ (x) > 0可得x >2或x <1，由f ′ (x) < 0可得1< x <2．

∴ 函数f ( x ) 的单调递增区间为 (0 ，1) 和 (2，+ ∞ )，

单调递减区间为 (1 , 2 )．                    …9分

(Ⅲ) 由(Ⅱ)可知函数f (x)在(0，1)单调递增，在(1，2)单调递减，在(2，+∞)单调递增．

且当x =1或x =2时，f ′ (x) = 0．                         

∴ f (x) 的极大值为 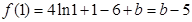       …10分       

f (x)的极小值为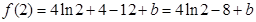    

由题意可知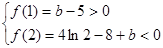 

则 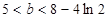                             ………11分

【解析】本试题主要考查了导数在研究函数中的运用，利用导数来判定函数的单调性，以及函数的零点的综合运用。

（1）函数f (x)的定义域为（0，+∞） ∵ f ′ (x) =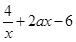 

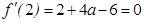∴，则a = 1

（2）由(Ⅰ) 知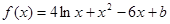

    ∴ f ′ (x) =解二次不等式得到单调区间。

（3）由(Ⅱ)可知函数f (x)在(0，1)单调递增，在(1，2)单调递减，在(2，+∞)单调递增．

且当x =1或x =2时，f ′ (x) = 0。