
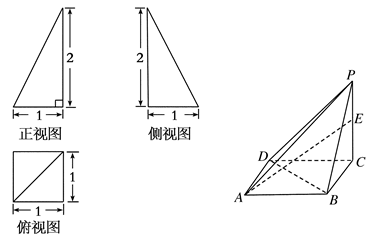
 (2)不论点E在何位置,都有BD⊥AE成立(3) 假设BF⊥平面PAD,
(2)不论点E在何位置,都有BD⊥AE成立(3) 假设BF⊥平面PAD,




 这与Rt△PAD中∠PDA为锐角矛盾.∴ BE不可能垂直于平面SCD
这与Rt△PAD中∠PDA为锐角矛盾.∴ BE不可能垂直于平面SCD ·PC·S底=
·PC·S底= ×2×1=
×2×1= . 3分
. 3分 ∴BD⊥平面PAC, 7分
∴BD⊥平面PAC, 7分 ,∴BD⊥AE恒成立. 8分
,∴BD⊥AE恒成立. 8分

 11分
11分
 ,
, 12分这与Rt△PAD中∠PDA为锐角矛盾.∴ BE不可能垂直于平面SCD 13分
12分这与Rt△PAD中∠PDA为锐角矛盾.∴ BE不可能垂直于平面SCD 13分 ,本题中在求解第二问第三问时还可通过空间向量的方法求解,根据已知条件可建立以点
,本题中在求解第二问第三问时还可通过空间向量的方法求解,根据已知条件可建立以点 为原点,
为原点, 为坐标轴的坐标系,通过直线的方向向量与平面的法向量判定线面位置关系
为坐标轴的坐标系,通过直线的方向向量与平面的法向量判定线面位置关系

科目:高中数学 来源:不详 题型:单选题
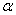 截一球面得圆M,过圆心M且与
截一球面得圆M,过圆心M且与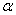 成
成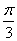 角的平面
角的平面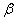 截该球面得圆N若圆M、圆N面积分别为4
截该球面得圆N若圆M、圆N面积分别为4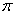 、13
、13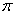 ,则球面面积为
,则球面面积为A.36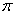 | B.48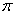 | C.64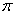 | D.100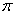 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com