练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知{an}为等差数列，且a3＝－6，a6＝0.

    （1）求{an}的通项公式；

    （2）若等比数列{bn}满足b1＝－8，b2＝a1＋a2＋a3，求{bn}的前n项和．

     


    解　(1)设等差数列{an}的公差为d.

    因为a3＝－6，a6＝0，

    所以

    解得a1＝－10，d＝2.

    所以an＝－10＋(n－1)×2＝2n－12.

    (2)设等比数列{bn}的公比为q.

    因为b2＝a1＋a2＋a3＝－24，b1＝－8，

    所以－8q＝－24，q＝3.

    所以数列{bn}的前n项和公式为

    Sn＝＝4(1－3n)．

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    求下列不等式的解集

                

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数与的图象上任意点P到直线的距离的最小值为       

    A.       B.        C.        D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设e1与e2是两个不共线向量，，若A、B、D

    三点共线，则k的值为(　　)

       A．－          B．－             C．  －          D．不存在

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    求值：_____________

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知全集U={﹣1，0，1，2，3，4}，A={﹣1，0，2，4}，则∁UA=（）

        A．             φ B．             {0，2，4}           C． {1，3}   D． {﹣1，1，3}

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    下列向量中，可以作为基底的是（）

        A．                                 =（0，0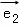），=（1，﹣2）  B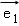． =（2，﹣3），=（﹣，）

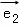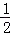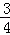        C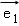．                                 =（3，5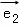），=（6，10）   D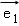． =（1，﹣2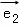），=（5，7）

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设函数f（x）=ax﹣（k﹣1）a﹣x（a＞0且a≠1）是定义域为R的奇函数．

    （1）若f（1）＞0，试判断函数f（x）的单调性，并求使不等式f（sin2θ+cos2θ）+f（1﹣tcosθ）＜0对所有的θ∈（0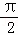，）均成立的t的取值范围；

    （2）若f（1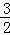）=，g（x）=a2x+a﹣2x﹣2mf（x），且g（x）在[1，+∞）上的最小值为﹣1，求m的值．

     

    查看答案和解析>>

    科目：高中数学 来源：2014-2015学年江苏省扬州市高三上学期期末理科数学试卷（解析版） 题型：解答题

    射击测试有两种方案，方案1：先在甲靶射击一次，以后都在乙靶射击；方案2：始终在乙靶射击，某射手命中甲靶的概率为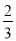，命中一次得3分；命中乙靶的概率为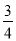，命中一次得2分，若没有命中则得0分，用随机变量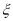表示该射手一次测试累计得分，如果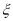的值不低于3分就认为通过测试，立即停止射击；否则继续射击，但一次测试最多打靶3次，每次射击的结果相互独立。

    （1）如果该射手选择方案1，求其测试结束后所得分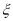的分布列和数学期望E；

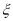    （2）该射手选择哪种方案通过测试的可能性大？请说明理由。

    查看答案和解析>>

    同步练习册答案