
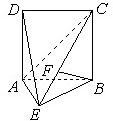
 如图,DA⊥平面ABE,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.
如图,DA⊥平面ABE,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.| 2 |
| 2 |
| BC2+BE2 |
| 6 |
| BC•BE |
| EC |
2
| ||
| 3 |
| BO2-BF2 |
| ||
| 3 |
| BF |
| OF |
| ||||
|
| 2 |
| 2 |


科目:高中数学 来源: 题型:
 (2013•汕尾二模)如图,四棱锥P-ABCD的底面ABCD为矩形,且PA=AD=1,AB=2,∠PAB=120°,∠PBC=90°.
(2013•汕尾二模)如图,四棱锥P-ABCD的底面ABCD为矩形,且PA=AD=1,AB=2,∠PAB=120°,∠PBC=90°.查看答案和解析>>
科目:高中数学 来源: 题型:
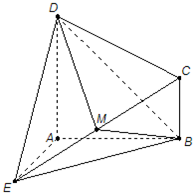 (2008•深圳一模)如图所示的几何体ABCDE中,DA⊥平面EAB,CB∥DA,EA=DA=AB=2CB,EA⊥AB,M是EC的中点.
(2008•深圳一模)如图所示的几何体ABCDE中,DA⊥平面EAB,CB∥DA,EA=DA=AB=2CB,EA⊥AB,M是EC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
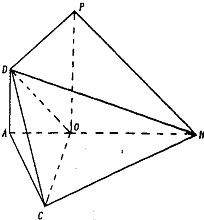 (2010•泰安二模)如图,在△ABC中,已知∠ABC=45°,O在AB上,且OB=OC=
(2010•泰安二模)如图,在△ABC中,已知∠ABC=45°,O在AB上,且OB=OC=| 2 |
| 3 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2008年广东地区数学科全国各地模拟试题直线与圆锥曲线大题集 题型:044
如图,在平面直角坐标系中,O为坐标原点,点B(0,1),且点A(a,0)(a≠0)是x轴上动点,过点A作线段AB的垂线交y轴于点D,在直线AD上取点P,使AP=DA

(1)求动点P的轨迹C的方程
(2)点Q是直线y=-1上的一个动点,过点Q作轨迹C的两条切线,切点分别为M,N,求证:QM⊥QN
查看答案和解析>>
科目:高中数学 来源:宁夏银川一中2009届高三年级第五次月考测试数学试卷(理) 题型:013
如图,在平面直角坐标系中,Ω是一个与x轴的正半轴、y轴的正半轴分别相切于点C、D的定圆所围成区域(含边界),A、B、C、D是该圆的四等分点,若点P(x,y)、P0(x0,y0)满足x≤x0且y≥y0,则称P优于P0,如果Ω中的点Q满足:不存在Ω中的其它点优于Q,那么所有这样的点Q组成的集合是劣弧

A.弧AB
B.弧BC
C.弧CD
D.弧DA
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com