
 ,
,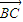 ∥
∥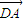 ,求x与y之间的关系式;
,求x与y之间的关系式;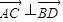 ,求向量
,求向量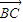 的模的大小.
的模的大小.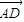 的坐标,又由
的坐标,又由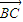 ∥
∥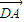 ,可得x(2-y)-y(-x-4)=0,变形可得答案;
,可得x(2-y)-y(-x-4)=0,变形可得答案;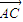 、
、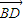 的坐标,又由
的坐标,又由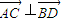 ,可得(x+6)(x-2)+(y+1)(y-3)=0①,结合(1)的结论x+2y=0②,联立①②,解可得x、y的值,可得
,可得(x+6)(x-2)+(y+1)(y-3)=0①,结合(1)的结论x+2y=0②,联立①②,解可得x、y的值,可得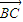 的坐标,进而计算可得|
的坐标,进而计算可得|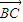 |,即可得答案.
|,即可得答案.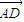 =
=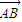 +
+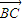 +
+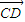 =(x+4,y-2),
=(x+4,y-2),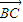 ∥
∥ ,则x(2-y)-y(-x-4)=0,
,则x(2-y)-y(-x-4)=0,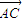 =(x+6,y+1),
=(x+6,y+1),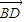 =(x-2,y-3),
=(x-2,y-3),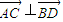 ,
,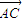 •
•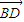 =0,(x+6)(x-2)+(y+1)(y-3)=0,①
=0,(x+6)(x-2)+(y+1)(y-3)=0,①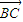 =(-6,3)或(2,-1);
=(-6,3)或(2,-1);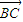 |=3
|=3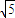 或
或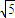 .
.

科目:高中数学 来源:湖北省期末题 题型:解答题
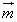 =(1,λsinA),
=(1,λsinA), =(sinA,1+cosA).已知
=(sinA,1+cosA).已知 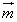 ∥
∥ .
.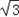 a,求λ的取值范围.
a,求λ的取值范围.查看答案和解析>>
科目:高中数学 来源:2012年浙江省高考数学仿真模拟试卷8(文科)(解析版) 题型:解答题
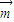 =(1,λsinA),
=(1,λsinA),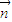 =(sinA,1+cosA).已知
=(sinA,1+cosA).已知 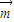 ∥
∥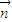 .
.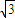 a,求λ的取值范围.
a,求λ的取值范围.查看答案和解析>>
科目:高中数学 来源:安徽省合肥市2010届高三第四次模拟(理) 题型:解答题
已知函数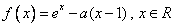 .
.
(1)若实数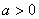 ,求函数
,求函数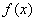 在
在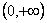 上的极值;
上的极值;
(2)记函数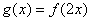 ,设函数
,设函数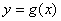 的图象C与
的图象C与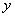 轴交于
轴交于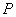 点,曲线C在
点,曲线C在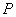 点处的切线与两坐标轴所围成的图形的面积为
点处的切线与两坐标轴所围成的图形的面积为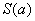 ,求当
,求当 时
时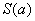 的最小值。
的最小值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com