
(本大题12分)
在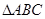 中,设角
中,设角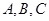 的对边分别是
的对边分别是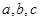 ,
,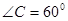 ,
,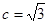 .
.
(Ⅰ)求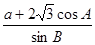 的值;
的值;
(Ⅱ)若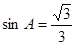 ,求
,求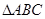 的面积.
的面积.
科目:高中数学 来源:2012-2013学年四川省成都市高新区高三2月月考理科数学试卷(解析版 题型:解答题
(本小题12分)在直三棱柱(侧棱垂直底面)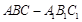 中,
中,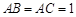 ,
,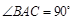 .
.
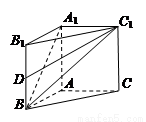
(Ⅰ)若异面直线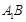 与
与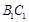 所成的角为
所成的角为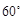 ,求棱柱的高;
,求棱柱的高;
(Ⅱ)设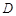 是
是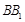 的中点,
的中点,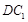 与平面
与平面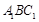 所成的角为
所成的角为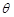 ,当棱柱的高变化时,求
,当棱柱的高变化时,求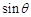 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江杭州高二12月月考理科数学试卷(解析版) 题型:解答题
(本大题12分)如图,在棱长为ɑ的正方体ABCD-A1B1C1D1中,E、F、G分别是CB、CD、CC1的中点.
(1)求直线 C与平面ABCD所成角的正弦的值;
C与平面ABCD所成角的正弦的值;
(2)求证:平面A B1D1∥平面EFG;
(3)求证:平面AA1C⊥面EFG .

查看答案和解析>>
科目:高中数学 来源:2010-2011学年四川省高三上学期10月月考文科数学卷 题型:解答题
(本大题12分)
为了迎接2010年10月1日国庆节,某城市为举办的大型庆典活动准备了四种保证安全的方案,列表如下:
|
方案 |
A |
B |
C |
D |
|
经费 |
300万元 |
400万元 |
500万元 |
600万元 |
|
安全系数 |
0.6 |
0.7 |
0.8 |
0.9 |
其中安全系数表示实施此方案能保证安全的系数,每种方案相互独立,每种方案既可独立用,又可以与其它方案合用,合用时,至少有一种方案就能保证整个活动的安全
(I)求A、B两种方案合用,能保证安全的概率;
(II)若总经费在1200万元内(含1200万元),如何组合实施方案可以使安全系数最高?
查看答案和解析>>
科目:高中数学 来源:2012届山东省兖州市高二下学期期末考试数学(文) 题型:解答题
(本小题12分)在对人们休闲的一次调查中,共调查了124人,其中女性70人
男性54人.女性中有43人主要的休闲方式是看电视,另外27人的休闲方式是运动;男性
中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动.
(1) 根据以上数据建立一个2×2的列联表;
(2)检验性别是否与休闲方式有关,可靠性有多大?
参考临界值如下
|
|
0.05 |
0.025 |
0.01 |
|
|
3.841 |
5.024 |
6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com