
某煤矿发生透水事故时,作业区有若干人员被困.救援队从入口进入之后有 两条巷道通往作业区(如下图),
两条巷道通往作业区(如下图), 巷道有
巷道有 三个易堵塞点,各点被堵塞的概率都是
三个易堵塞点,各点被堵塞的概率都是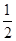 ;
; 巷道有
巷道有 两个易堵塞点,被堵塞的概率分别为
两个易堵塞点,被堵塞的概率分别为 .
.
(1)求 巷道中,三个易堵塞点最多有一个被堵塞的概率;
巷道中,三个易堵塞点最多有一个被堵塞的概率;
(2)若 巷道中堵塞点个数为
巷道中堵塞点个数为 ,求
,求 的分布列及数学期望
的分布列及数学期望 ,并按照"平均堵塞点少的巷道是较好的抢险路线"的标准,请你帮助救援队选择一条抢险路线,并说明理由.
,并按照"平均堵塞点少的巷道是较好的抢险路线"的标准,请你帮助救援队选择一条抢险路线,并说明理由.
(1)三个易堵塞点最多有一个被堵塞的概率为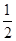 ;(2)选择
;(2)选择 巷道为抢险路线为好,该巷道平均堵塞点少.
巷道为抢险路线为好,该巷道平均堵塞点少.
解析试题分析:(1)
科目:高中数学
来源:
题型:解答题
商场销售的某种饮品每件售价为36元,成本为20元.对该饮品进行促销:顾客每购买一件,当即连续转动三次如图所示转盘,每次停止后指针向一个数字,若三次指向同一个数字,获一等奖;若三次指向的数字是连号(不考虑顺序),获二等奖;其他情况无奖.
科目:高中数学
来源:
题型:解答题
某中学在高一开设了数学史等4门不同的选修课,每个学生必须选修,且只能从中选一门.该校高一的3名学生甲、乙、丙对这4门不同的选修课的兴趣相同.
科目:高中数学
来源:
题型:解答题
如图,从A1(1,0,0)、A2(2,0,0)、B1(0,1,0)、B2(0,2,0)、C1(0,0,1)、C2(0,0,2)这6个点中随机选取3个点,将这3个点及原点O两两相连构成一个“立体”,记该“立体”的体积为随机变量V(如果选取的3个点与原点在同一个平面内,此时“立体”的体积V=0).
科目:高中数学
来源:
题型:解答题
黄山旅游公司为了体现尊师重教,在每年暑假期间对来黄山旅游的全国各地教师和学生,凭教师证和学生证实行购买门票优惠.某旅游公司组织有22名游客的旅游团到黄山旅游,其中有14名教师和8名学生.但是只有10名教师带了教师证,6名学生带了学生证.
科目:高中数学
来源:
题型:解答题
对某电子元件进行寿命追踪调查,所得情况如右频率分布直方图.
科目:高中数学
来源:
题型:解答题
小波以游戏方式决定是参加学校合唱团还是参加学校排球队,游戏规则为:以0为起点,再从
科目:高中数学
来源:
题型:解答题
甲乙两人进行乒乓球比赛,各局相互独立,约定每局胜者得1分,负者得0分,如果两人比赛五局,乙得1分与得2分的概率恰好相等.
科目:高中数学
来源:
题型:解答题
一盒中装有零件12个,其中有9个正品,3个次品,从中任取一个,如果每次取出次品就不再放回去,再取一个零件,直到取得正品为止.求在取得正品之前已取出次品数的期望.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区 巷道中,三个易堵塞点最多有一个被堵塞的概率
巷道中,三个易堵塞点最多有一个被堵塞的概率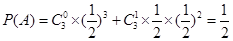 ;
;
(2)若 巷道中堵塞点个数为
巷道中堵塞点个数为 ,先写出
,先写出 的分布列,根据分布列求出数学期望
的分布列,根据分布列求出数学期望 ,同样的方法求出
,同样的方法求出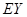 ,而
,而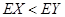 ,所以选择
,所以选择 巷道为抢险路线为好.
巷道为抢险路线为好.
试题解析:(1)设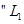 巷道中,三个易堵塞点最多有一个被堵塞
巷道中,三个易堵塞点最多有一个被堵塞 为事件
为事件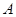
则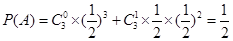
(2)依题意, 的可能取值为0,1,2
的可能取值为0,1,2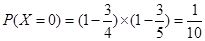
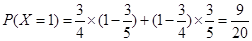
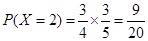
所以,随机变量 的分布列为:
的分布列为:
0 1 2 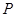
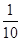
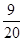
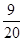
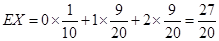
(方法一)设 巷道中堵塞点个数为
巷道中堵塞点个数为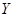 ,则
,则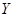 的可能取值为0,1,2,3
的可能取值为0,1,2,3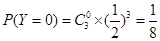
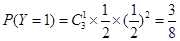
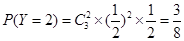
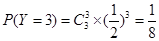
所以,随机变量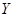 的分布列为:
的分布列为: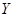
0 1 2 3 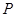
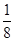


1加1阅读好卷系列答案
专项复习训练系列答案
初中语文教与学阅读系列答案

完形填空与阅读理解周秘计划系列答案
英语阅读理解150篇系列答案
奔腾英语系列答案
标准阅读系列答案
53English系列答案
考纲强化阅读系列答案
(1)求一顾客一次购买两件该饮品,至少有一件获得奖励的概率;
(2)若奖励为返还现金,一等奖奖金数是二等奖的2倍,统计表明:每天的销售y(件)与一等奖的奖金额x(元)的关系式为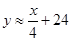 ,问x设定为多少最佳?并说明理由.
,问x设定为多少最佳?并说明理由.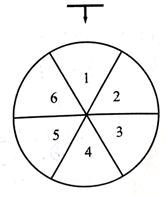
(1)求3个学生选择了3门不同的选修课的概率;
(2)求恰有2门选修课这3个学生都没有选择的概率;
(3)设随机变量X为甲、乙、丙这三个学生选修数学史这门课的人数,求X的分布列.
(1)求V=0的概率;
(2)求V的分布列及数学期望E(V).
(1)在该旅游团中随机采访3名游客,求恰有1人持有教师证且持有学生证者最多1人的概率;
(2)在该团中随机采访3名学生,设其中持有学生证的人数为随机变量ξ,求ξ的分布列.
(1)图中纵坐标 处刻度不清,根据图表所提供的数据还原
处刻度不清,根据图表所提供的数据还原 ;
;
(2)根据图表的数据按分层抽样,抽取 个元件,寿命为
个元件,寿命为 之间的应抽取几个;
之间的应抽取几个;
(3)从(2)中抽出的寿命落在 之间的元件中任取
之间的元件中任取 个元件,求事件“恰好有一个寿命为
个元件,求事件“恰好有一个寿命为 ,一个寿命为
,一个寿命为 ”的概率.
”的概率. ,
, (如图)这8个点中任取两点分别分终点得到两个向量,记这两个向量的数量积为X。若X=0就参加学校合唱团,否则就参加学校排球队。
(如图)这8个点中任取两点分别分终点得到两个向量,记这两个向量的数量积为X。若X=0就参加学校合唱团,否则就参加学校排球队。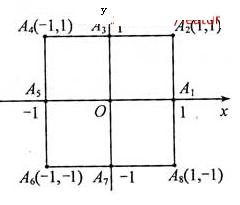
(1)求小波参加学校合唱团的概率;
(2)求X的分布列和数学期望.
求乙在每局中获胜的概率为多少?
假设比赛进行到有一人比对方多2分或打满6局时停止,用 表示比赛停止时已打局数,求
表示比赛停止时已打局数,求 的期望
的期望 .
.
版权声明:本站所有文章,图片来源于网络,著作权及版权归原作者所有,转载无意侵犯版权,如有侵权,请作者速来函告知,我们将尽快处理,联系qq:3310059649。
ICP备案序号: 沪ICP备07509807号-10 鄂公网安备42018502000812号