练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    （本小题共13分）
    如图，在四棱锥P—ABCD中，PA⊥平面ABCD，底面ABCD为直角梯形，∠ABC=
    ∠BAD=90°，AD＞BC，E，F分别为棱AB，PC的中点.
    （I）求证：PE⊥BC；
    （II）求证：EF//平面PAD.

    （I）证明见解析。
    （II）证明见解析。

    解析证明：（I）
    ∴PA⊥BC


    ∴BC⊥平面PAB
    又E是AB中点，
    平面PAB
    ∴BC⊥PE.                                                                                     …………6分
    （II）证明：取CD中点G，连结FG，EG，

    ∵F为PC中点，∴FG//PD

    ∴FG//平面PAD；
    同理，EG//平面PAD

    ∴平面EFG//平面PAD.
    ∴EF//平面PAD.                                                                            …………13分

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （本小题共13分）

       如图，在四棱锥P—ABCD中，PA⊥平面ABCD，底面ABCD为直角梯形，∠ABC=

    ∠BAD=90°，为AB中点，F为PC中点.

       （I）求证：PE⊥BC；

       （II）求二面角C—PE—A的余弦值；

       （III）若四棱锥P—ABCD的体积为4，求AF的长.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （本小题共13分）

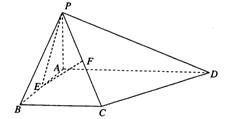
        如图，在四棱锥P—ABCD中，PA⊥平面ABCD，底面ABCD为直角梯形，∠ABC=

    ∠BAD=90°，AD＞BC，E，F分别为棱AB，PC的中点.

       （I）求证：PE⊥BC；

       （II）求证：EF//平面PAD.

    查看答案和解析>>

    科目：高中数学 来源：北京市宣武区2010年高三第一次质量检测数学（理）试题 题型：解答题

    （本小题共13分）

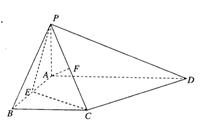
       如图，在四棱锥P—ABCD中，PA⊥平面ABCD，底面ABCD为直角梯形，∠ABC=

    ∠BAD=90°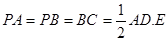，为AB中点，F为PC中点.

       （I）求证：PE⊥BC；

       （II）求二面角C—PE—A的余弦值；

       （III）若四棱锥P—ABCD的体积为4，求AF的长.

     

    查看答案和解析>>

    科目：高中数学 来源：北京市宣武区2010年高三第一次质量检测数学（文）试题 题型：解答题

    （本小题共13分）

        如图，在四棱锥P—ABCD中，PA⊥平面ABCD，底面ABCD为直角梯形，∠ABC=

    ∠BAD=90°，AD＞BC，E，F分别为棱AB，PC的中点.

       （I）求证：PE⊥BC；

       （II）求证：EF//平面PAD.

     

    查看答案和解析>>

    科目：高中数学 来源：2007年普通高等学校招生全国统一考试理科数学卷（北京） 题型：解答题

    （本小题共13分）

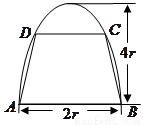    如图，有一块半椭圆形钢板，其半轴长为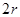，短半轴长为，计划将此钢板切割成等腰梯形的形状，下底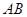是半椭圆的短轴，上底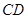的端点在椭圆上，记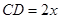，梯形面积为．

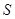    （I）求面积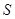以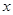为自变量的函数式，并写出其定义域；

    （II）求面积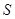的最大值．

     

     

     

     

    查看答案和解析>>

    同步练习册答案