Question

与圆，圆同时外切的动圆圆心的轨迹方程是_____________。

Answer 1

 

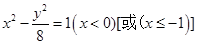
解析试题分析：根据题意可知，设动圆的圆心为P，半径为r，
而圆（x-3）²+y²=9的圆心为M₁（3，0），半径为3；
圆（x+3）²+y²=1的圆心为M₂（-3，0），半径为1
依题意得|PM₁|=3+r，|PM₂|=1+r，
则|PM₁|-|PM₂|=（3+r）-（1+r）=2＜|M₁M₂|，
所以点P的轨迹是双曲线的右支．
且：a=1，c=3，b²=8
其方程是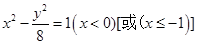：，。答案为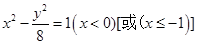
考点：本题主要考查了查双曲线的定义．本题考查的知识点是圆的方程、椭圆的性质及椭圆与直线的关系。
点评：解题的关键是根据已知条件中未知圆与已知圆的位置关系，结合“圆的位置关系与半径及圆心距的关系”，探究出动圆圆心P的轨迹，进而给出动圆圆心P的轨迹方程．