
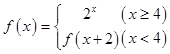 ,则
,则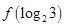 = 。
= 。科目:高中数学 来源:不详 题型:解答题
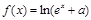 (
(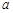 为常数)是实数集
为常数)是实数集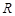 上的奇函数,函数
上的奇函数,函数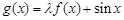 是区间
是区间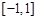 上的减函数。
上的减函数。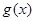 在
在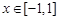 上的最大值;
上的最大值;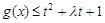 对
对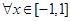 及
及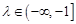 恒成立,求
恒成立,求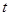 的取值范围;
的取值范围;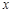 的方程
的方程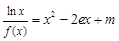 的根的个数。
的根的个数。查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
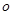 的函数关系式为:
的函数关系式为: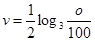 。若某条鱼想把游速提高1 m/s,它的耗氧量将增大到原来的a倍,则a=
。若某条鱼想把游速提高1 m/s,它的耗氧量将增大到原来的a倍,则a=| A.9 | B.8 | C.3 | D.2 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
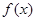 的边际函数
的边际函数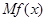 定义为
定义为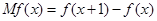 .某公司每月最多生产100台报警系统装置,生产
.某公司每月最多生产100台报警系统装置,生产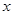 台(
台(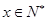 )的收入函数为
)的收入函数为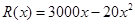 (单位:元),其成本函数为
(单位:元),其成本函数为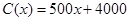 (单位:元),利润是收入与成本之差.
(单位:元),利润是收入与成本之差.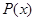 及边际利润函数
及边际利润函数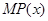 的解析式,并指出它们的定义域;
的解析式,并指出它们的定义域;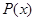 与边际利润函数
与边际利润函数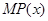 是否具有相同的最大值?说明理由;
是否具有相同的最大值?说明理由; 查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
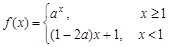 在
在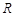 上单调递减,则实数
上单调递减,则实数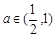 ;②若函数
;②若函数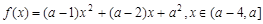 是偶函数,则实数
是偶函数,则实数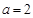 ;③若函数
;③若函数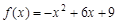 在区间
在区间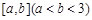 上有最大值9,最小值
上有最大值9,最小值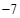 ,则
,则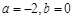 ;④
;④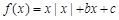 的图象关于点
的图象关于点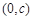 对称。其中正确的序号有 。
对称。其中正确的序号有 。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com